logo

Testing the Validity of Purchasing Power Parity for Syria: Evidence from Non-Linear Unit Root Tests

2023-08-19 | Volume 1 Issue 2 - Volume 1 | Research Articles | Linda Ali Ismaiel

Abstract

This study aims to examine the empirical validity of Purchasing Power Parity (PPP) hypothesis for Syria in the context of unit root tests based on linear and non-linear models. For this purpose, the author uses both the official as well as the parallel real exchange rates of the Syrian Pound against the US dollar from 2011:04 to 2020:08. In addition to conventional unit root tests without and with structural breaks, the nonlinear unit root tests of Kapetanios et al, Kruse, Kılıç and Sollis are applied to test the stationarity of real exchange rates, and hence the validity of PPP. The empirical results reveal that, in contrast to conventional unit root tests, the nonlinear unit root tests provide highly strong evidence in favor of PPP for both real exchange rate series under consideration. These findings signify the importance of accounting for non-linearity to analyze the behavior of real exchange rates in Syria.

Keywords : Purchasing Power Parity, Real Exchange Rate, Nonlinearity, Unit Root Test, Syria.

INTRODUCTION

Despite being broadly examined in the literature, purchasing power parity (PPP) is still at the center of attention due to the lack of consensus on its empirical validity. The relative version of the PPP postulates that changes in the nominal exchange rate between a pair of currencies should be proportional to the relative price levels of the two countries concerned. When PPP holds, the real exchange rate, defined as the nominal exchange rate adjusted for relative national price level differences, is a constant [1].

Tests conducted to validate the PPP have developed pari passu with advances in econometric techniques. A major strand of this literature focused on the stationarity of real exchange rates as stationary implies mean reversion and, hence, PPP. Earlier studies that analyzed the stationarity of real exchange rate are generally based on linear conventional unit root tests, such as the augmented dickey fuller (ADF), the Phillip Perrons (PP) and the Kwiatkowski, Phillips, Schmidt and Shin (KPSS). However, these unit root tests suffer from low power for finite samples. To address this problem, a new trend of studies started applying long-span data sets. Nonetheless, a potential problem with these studies is that the long-span data may be inappropriate because of possible regime shifts and differences in real exchange rate behavior [1,2]. To overcome this potential problem, an innovation was made possible by the appearance of unit root tests that allow for one or multiple structural breaks, such as Perron (1989), Zivot and Andrews (1992), Lumsdaine and Papell (1997) and Lee and Strazicich, (2003, 2004) test [3-7].

Another approach undertaken by the literature to circumvent the problem of low-power is to apply panel unit root techniques in the empirical tests of PPP. One criticism of these tests relates to the fact that rejecting the null hypothesis of a unit root implies that at least one of the series is stationary, but not that all the series are mean reverting [8,9].

The issues raised by the long-span and the panel-data studies explain the first PPP puzzle.
A second related puzzle also exists. It is summarized in Rogoff (1996) as follows: “How can one reconcile the enormous short-term volatility of real exchange rates with the extremely slow rate at which shocks appear to damp out?”[10]. Based on the theoretical models of Dumas and Sercu et al, this second PPP puzzle introduced the idea that the real exchange rate might follow a nonlinear adjustment toward the long-run equilibrium due to transactions costs and trade barriers [11,12].

Recognizing the low power of conventional unit root tests in detecting stationarity of real exchange rates with nonlinear behavior, new testing approaches have emerged, which consider the nonlinear processes explicitly. Among others, Obstfeld and Taylor (1997) [13], Enders and Granger (1998) [14] and Caner and Hansen (2001) [15] suggested to investigate the nonlinear adjustment process in terms of a threshold autoregressive (TAR) model. This model allows for a transactions costs band within which arbitrage is unprofitable as the price differentials are not large enough to cover transaction costs. However, once the deviation from PPP is sufficiently large, arbitrage becomes profitable, and hence the real exchange rate reverts back to equilibrium [13,16]. More specifically, real exchange rate tends to revert back to equilibrium only when it is sufficiently far away from it, which implies that it has a nonlinear adjustment toward the long-run equilibrium [9,17-19].

While transaction costs have most often been advanced as possible contributors to nonlinearity in real exchange rates, it is argued that nonlinearity may also arise from heterogeneity in agents’ opinions in foreign exchange rate markets. As discussed in Taylor and Taylor [20], as nominal exchange rates have extreme values, a greater degree of consensus concerning the appropriate direction of exchange rates prevails, and international traders act accordingly.

Official intervention in the foreign exchange market when the exchange rate is away from equilibrium is another argument for the presence of nonlinearities [20]. According to Bahmani-Oskooee and Gelan, we expect a higher degree of nonlinearity in the official real exchange rates of less developed countries compared to those of developed countries due to a higher level of intervention in the foreign exchange market in the former [21].

In the presence of transaction costs, heterogeneous agents and intervention of monetary authorities, many of authors (e.g., Dumas [11]; Terasvirta, [22]; Taylor et al [17]) suggest that the nonlinear adjustment of real exchange rate is smoother rather than instantaneous. One way to allow for smooth adjustment is to employ a smooth transition autoregressive (STAR) model that assumes the structure of the model changes as a function of a lag of the dependent variable [23].

In this context, Kapetanious et al developed a unit root test that has a specific exponential smooth transition autoregressive (ESTAR) model to examine the null hypothesis of non-stationarity against the alternative of nonlinear stationarity [16]. This model suggests a smooth adjustment towards a long-run attractor around a symmetric threshold band. Hence, small shocks with transitory effects would keep the exchange rate inside the band, while large shocks would
push the exchange rate outside the band. Once this band is exceeded, the series would display mean-reverting behavior. The jump outside the band is supposed to be corrected gradually [16].

More recently, modified versions of the nonlinear unit root test of Kapetanious et al, KSS) were proposed by Kılıç and Kruse [19,24]. Both studies observe that their modified tests are in most situations superior in terms of power to the Dickey-Fuller type test proposed by Kapetanios et al. Sollis proposed another extension of ESTAR model, the asymmetric exponential smooth transition auto-regressive (AESTAR) model, where the speed of adjustment could be different below or above the threshold band [25].

Recently, the effect of non-linearity has become popular in testing the validity of PPP (e.g., [9,17,26-31]). These studies provided stronger evidence in favor of PPP compared to the previous studies using conventional unit root tests.

The attention given to testing PPP in Syria has so far been very limited. Hassanain examined the PPP in 10 Arab countries, including Syria, from 1980 to 1999. Using panel unit root tests, he found evidence in favor of the PPP [32]. El-Ramely tested the validity of PPP in a panel of 12 countries from the Middle East, including Syria, for the period 1969-2002. She found that the evidence in support of PPP is generally weak [33]. Cashin and Mcdermott examined the PPP hypothesis for 90 developed and developing countries, including Syria, for the period 1973-2002 [34]. For this purpose, they utilized real effective exchange rates and applied the median-unbiased estimation techniques that remove the downward bias of least squares. The findings provided evidence in favor of the PPP in the majority of countries. Kula et al tested the validity of PPP for a sample of 13 MENA countries, including Syria. For this purpose, they applied Lagrange Multiplier unit root test that endogenously determines structural breaks, using official and black exchange rate data over 1970-1998. The empirical results indicated that the PPP holds for all countries when the test with two structural breaks is applied [35]. Al-Ahmad and Ismaiel examined the PPP using monthly data of the real effective exchange rates in 4 Arab countries, including Syria, from 1995 to 2014. For this purpose, the authors applied unit root tests that account for endogenous structural breaks in the data, those being the Zivot and Andrews test and the Lumsdaine and Papell tests. The results indicated that the unit root null hypothesis could be rejected for Syria only when the Lumsdaine and Papell three structural break test was applied and at the 10% level of significance [36].

The scarcity of research that focused on Syria during the recent period of crisis and the fact that the validity of the PPP hypothesis depends largely on the period of analysis, the type of data used and the econometric tests applied, motivated further testing of the PPP for this country.

The purpose of this study is to test the PPP hypothesis for Syria using more recent data that includes the recent crisis that erupted in 2011 in the context of unit root tests based on linear and non-linear models of the real exchange rate.

The current study makes three main contributions to the literature; first, it tests the validity of the PPP hypothesis by examining monthly real exchange rates of the Syrian pound against the US dollar over the period 2011:04-2020:08. This period is characterized by deterioration in the economic fundamentals and sharp currency depreciation as a result of the crisis that erupted on March 2011. Given developments in the official rate, the emergence of a parallel market, and a newly implemented intervention rate, the International Monetary Fund changed the classification of the exchange rate arrangement of Syria from “stabilized arrangement” to “other managed arrangement” on April 2011. Worth noting that Syria maintains during the period of study a multiple currency practice resulting from divergences of more than 2% between the official exchange rate and officially recognized market exchange rates [37].

Second, this study uses both the official and the parallel exchange rates in testing the PPP, which fills an important gap in the literature of PPP. In fact, studies concerning PPP mostly used the official exchange rates, especially in less developed countries. However, as outlined by Bahmani-Oskooee and Gelan, the official exchange rates may bias the inferences concerning the validity of PPP in the countries with significant black-market activities [21]. More specifically, due to restrictions on foreign currencies in Syria, these currencies are more expensive on the black market. The black-market or parallel exchange rate would thus reflect actual supply and demand pressures, and testing the validity of PPP in this context may indicate whether the foreign exchange market is efficient [38].

Third, in addition to conventional unit root tests, the nonlinear unit root tests of Kapetanios et al, Kruse, Kılıç and Sollis are applied to account for the possible nonlinearity that may arise from transaction costs, trade barriers and frequent official interventions in the foreign exchange market. As pointed out in Bahamani-Oskooee and Hegerty [38], nonlinear tests can be particularly useful in a study of less developed countries that face both external and internal shocks, such as periods of high inflation and sharp depreciation or devaluation of the exchange rate, which is the case of the Syrian economy. To our best knowledge, this study is the first that employs these nonlinear unit root tests to examine the validity of PPP for Syria over the period of crisis that erupted on March 2011.

The findings of this study should provide new evidence on the behavior of exchange rates in Syria during the recent period of crisis, which should be of interest to economists, policy makers and exchange rate market participants. As outlined by Taylor, the more important problem is to explain what drives the short-run dynamics of real exchange rates and how we account for the persistence of deviations from PPP in different time periods [39]. More specifically, knowing whether the PPP holds and if the real exchange rates follow a global stationary nonlinear process is important to specify the nature of chocks to the real exchange rate and the appropriate policy response.

MATERIALS AND METHODS

 Data

To test the validity of PPP for Syria, the study applies monthly time series data of the natural logarithm of real exchange rate of the Syrian Pound against the US dollar from 2011:04 to 2020:08.

The importance of using the bilateral exchange rate against the dollar emerges from the fact that internal foreign exchange market is dollar dominated.

The real exchange rate is constructed as: RER =EX * (CPIUS / CPISY)

Where RER is the Real Exchange Rate, EX is the nominal Exchange Rate (measured as the price of the Syrian Pound relative to one unit of the US Dollar), and CPIUS and CPISY are the foreign and domestic consumer price indices (based on 2010=100), respectively.

We use both the official as well as the parallel real exchange rates against the US dollar. The real official exchange rate (RERoff) is constructed using the nominal official exchange rate (EXoff), while the real parallel exchange rate (RERPar) is constructed using the nominal parallel exchange rate (EXPar). All the series are plotted in Figure 1.

Data of the nominal exchange rates and the CPISY were collected from the Central Bank of Syria CBS (Data of the nominal official exchange rate were collected from the CBS website (available at https://www.cb.gov.sy/index.php?page=list&ex=2&dir=exchangerate&lang=1&service=4&act=1207). Data of the nominal parallel exchange rate (2011-0ctobre 2019) were obtained from the CBS upon request. Data of CPISY (2010=100) were collected from the CBS website for the period (2014:01-2020:08) (available at https://www.cb.gov.sy/index.php?page=list&ex= 2&dir=publications&lang=1&service=4&act=565). Data of CPISY (2010=100) for the period (2011:04-2013:12) were obtained from the CBS upon request because available data at the website are based on (2005=100) for this period. Note that data of CPISY are not available after 2020:08.). Data of the CPIUS were collected from the International Monetary Fund (Available at https://data.imf.org/regular.aspx?key=61015892).

Methods

To test the presence of a unit root in the exchange rate series, conventional unit root tests without structural breaks (ADF and PP) are first applied. However, these tests don’t take into account the presence of structural breaks in the data. In order to capture the structural breaks in the data, we employ the Lee and Strazicich one and two break unit root tests based on LM test.

While conventional and breakpoint unit root tests are applied, the data is assumed to be linear. Therefore, Kapetanios et al, Kruse, Kılıç and Sollis nonlinear unit root tests are applied based on the smooth transition autoregressive (STAR) model.

The Lee and Strazicich tests

Lee and Strazicich proposed using a minimum Lagrange Multiplier LM test for testing the presence of a unit root with one and two structural breaks. For this purpose, two models are considered; model A which allows for structural break in the intercept under the alternative hypothesis, and model C which allows for structural break in both the intercept and trend under the alternative hypothesis.

Nonlinear unit root test of Kapetanios et al

Kapetanios et al developed a procedure to detect the presence of non-stationarity against nonlinear but globally stationary exponential smooth transition autoregressive ESTAR processes. To this end, the following specific ESTAR model is used [16]:

∆yt= γyt-1[1-exp(-өy2t-1)] +ℇt           (1)

Where ө (the slope parameter) is zero under the null hypothesis of unit root and positive under the alternative hypothesis of the stationary ESTAR process. Kapetanios et al. (2003) use first-order Taylor series approximation to the ESTAR model under the null and get the following auxiliary regression:

∆yt=δY3t-1+error                       (2)

Noting that the demeaned data is used for the case with nonzero mean, and the demeaned and detrended data for the case with nonzero mean and nonzero linear trend.

Assuming that the errors in equation 1 are serially correlated and that they enter in a linear fashion, then Kapetanios et al. (2003) extend model (1) to:

∆yt= j∆yt-j+ γyt-1[1-exp(-өy2t-1)] +ℇt            (3)

The null hypothesis is tested against the alternative hypothesis by the tNL statistic:

          tNL= /s.e ( )                       (4)

Where δ ̂is the OLS estimate of δ and (s.e ( )) is the standard error of ( ) obtained from the following regression with p augmentation [16]:

∆yt= j∆yt-j+ δy3t-1+error             (5)

With δ ̂is zero under the null hypothesis of unit root and negative under the alternative hypothesis.

Nonlinear unit root test of Kruse

Kruse extended the unit root test of Kapetanios et al by allowing for a nonzero attractor c in the exponential transition function. The degree of mean reversion of the real exchange rate depended on the distance of the lagged real exchange rate from this attractor [9].

To this end, he considers the following nonlinear time series model:

∆yt= γyt-1(1-exp {-ө (yt-1-c )2}) +ℇt                   (6)

As in Kapetanios et a, Kruse applied a first- order Taylor approximation around ө=0, and imposes β3 =0. The following regression was hence obtained:

       ∆yt= β1y3t-1+ β2y2t-1 +ut                       (7)

With ut being a noise term depending on ℇt.

In the regression 7, the null hypothesis of a unit root was H0: β1 = β2 = 0 and the alternative hypothesis of a globally stationary ESTAR process was H1: β1 < 0, β2 ≠ 0. Note that a standard Wald test wasn’t appropriate as one parameter is one-sided under H1 while the other one is two-sided [19]. To overcome this problem, Krus drived a modified Wald test that built up on the inference techniques by Abadir and Distaso [40]:

         Ί=t2ß1/2=0+1( ˂0) t2ß1=0                     (8)

Where t2ß1/2=0 represents the squared t-statistic for the hypothesis ß1/2= 0 with ß1/2 being orthogonal to β1. The second term t2ß1 is a squared t-statistic for the hypothesis β1 = 0.

Nonlinear unit root test of Kılıç

Kılıç considered an ESTAR model where the transition variable was the lagged changes of the dependent variable. Once appreciations or depreciations were large enough, real exchange rates may adjust towards equilibrium level due to profitable arbitrage.

The unit root test proposed was based on a one-sided t statistic where the t-statistic was optimized over the transition parameter space (γ). Kılıç specifies the following model, under the assumption that serially correlated errors entered in a linear way [24]:

∆yt= i∆yt-i+ Φyt-1[1-exp(-γz2t)] +ℇt                 (9)

With:  Zt= ∆yt-d

The null and alternative hypotheses were set as H0: Φ= 0 against H1: Φ< 0.

As γ was unidentified under the unit root null hypothesis, Kılıç suggested to use the lowest possible t-value over a fixed parameter space of γ values that were normalized by the sample standard deviation of the transition variable zt.

Nonlinear unit root test of Sollis

ESTAR models assumed symmetrical adjustment in exchange rates towards PPP for the same size of a deviation, regardless of whether the real exchange rate was below or above the mean. However, appreciations and depreciations may lead to different speed of adjustment towards PPP [25].

Sollis proposed a test based on asymmetric exponential smooth transition autoregressive (AESTAR), where the speed of adjustment could be different below or above the threshold band.

The extended ESTAR process was as follows [25]:

∆yt=Φ1 y3t-1+Φ2 y4t-1+ i∆yt-i+ηi               (10)

In the case of the rejection of the unit root hypothesis (Φ1= Φ2=0), the symmetric hypothesis, (Φ2=0) will be tested against the asymmetric alternative hypothesis, Φ2≠ 0. The hypothesis may be tested for the zero mean, non-zero mean and deterministic trend cases.

RESULTS

Prior to applying the nonlinear unit root tests, conventional linear unit root tests, which do not take into account any structural breaks, are first used. We initially employ the Augmented Dickey-Fuller (ADF) and the Phillips and Perron (PP). The null hypothesis is a unit root for these two tests.

The findings, presented in Table 1, indicate the random walk behavior of both the official and the parallel exchange rates series.

Table 1: Conventional Linear Unit Root Tests Results  
ADF PP
Constant Constant and trend Constant Constant and trend
LRERoff -1.95 (0) -2.28 (0) -2.09 (2) -2.29 (0)
LRERpar -0.60 (3) -1.96 (3) -1.48 (7) -3.03 (3)

Source: Own computation (E-Views)

Notes: The lag length of the tests are reported in brackets. The optimal lag length of the ADF test was selected based on the modified AIC (MAIC). The bandwidth for the PP test were selected based on Newey-West automatic bandwidth selection procedure for a Bartlett kernel. The critical values for ADF and PP tests are -3.49 (1%), -2.89 (5%) and -2.58 (10%) for model with constant; and -4.05 (1%), -3.45 (5%) and -3.15 (10%) for the model with constant and trend.

To account for the power loss in the presence of structural breaks, we employ the Lee and Strazicich one and two break unit root tests. The relevance of using this approach is that it is unaffected by breaks under the null. According to the results reported in Table 2, we cannot reject the null hypothesis at the 5% level of significance, regardless of whether we use official or parallel official exchange rates. The null hypothesis could be rejected only for the official exchange rate after allowing for two breaks in the constant and trend and at the 10% level of significance. Note that the estimated break dates appear to vary concerning the model specification and data used.

These findings are consistent with those of Al-Ahmad and Ismaiel [36], who found that the unit root null hypothesis of Lumsdaine and Papell test could be rejected for the real effective exchange rates of the Syrian Pound only after allowing for three changes in the constant and trend and at the 10% level of significance.

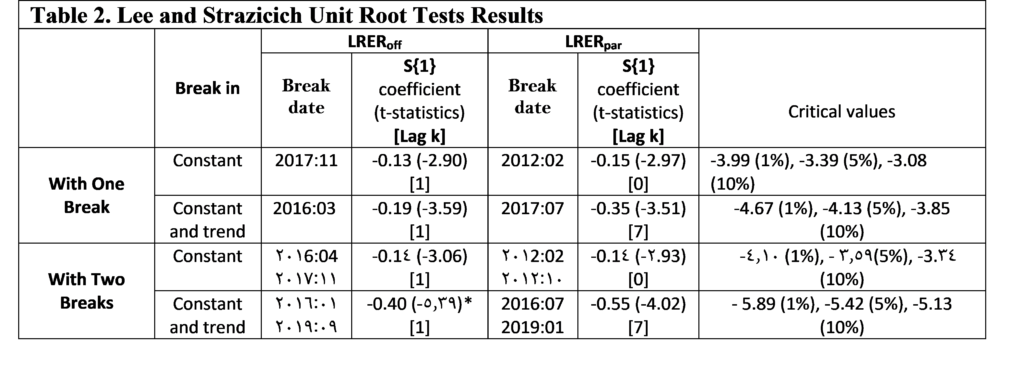Source: Own computation (E-Views)

Notes: The coefficient of S{1} tests for the unit-root. The T-statistics are reported in brackets. The optimal lag length is determined by GTOS method. ***, **, * denote rejection of the null hypothesis of a unit root at 1%, 5% and 10% level of significance respectively.

We now test whether taking into account for non-linearity in the real exchange rates plays a role in analyzing unit root dynamics. Prior to this, we checked the nonlinearity of the series by using the conventional BDS test proposed by Broock et al [41]. According to the results, a nonlinear nature was detected in both series, which makes relevant to apply nonlinear unit root test (Results from the BDS test are not presented here but available upon request). To this end, we proceed with the non-linear unit root tests developed by Kapetanios et al. (2003), Kruse (2011), Kılıç (2011) and Sollis (2009). The results of test statistics are reported in Table 3.

Table 3: Nonlinear Unit Root Tests Results
The nonlinear unit root test LRERoff LRERpar Critical values
1% 5% 10%
Kapetanios et al. (2003) Demeaned data -5.82***(1) -5.03***(1) -3.48 -2.93 -2.66
Detrended data -6.58***(1) -6.83***(1) -3.93 -3.40 -3.13
Sollis (2009) Demeaned data 25.74***(1) 16.51***(1) 6.89 4.88 4.00
Detrended data 22.62 ***(1) 23.18***(1) 8.80 6.55 5.41
Kılıç (2011) Demeaned data -2.23*(1) -1.58 (1) -2.98 -2.37 -2.05
Detrended data -2.61**(1) -2.99**(1) -3.19 -2.57 -2.23
Kruse (2011) Demeaned data 44.35***(1) 33.24***(1) 13.75 10.17 8.60
Detrended data 42.97***(1) 47.47***(1) 17.10 12.82 11.10

Source: Own computation (R for windows)

Notes: The lag length of the tests are reported in brackets. For all tests, the order of lags was chosen according to the Akaike information criterion (AIC).  Table critical values of unit root tests are taken from KSS (2003)[16], Sollis (2009)[25], Kılıç (2011)[24] and Kruse (2011)[19]. ***, **, * denote rejection of the null hypothesis of a unit root at 1%, 5% and 10% level of significance respectively.

The results of Kapetanios et al and Kruse showed that the null of unit root was rejected at the 1% level of significance for both official and parallel exchange rate, regardless of whether we use model with demeaned or detrended data. We also rejected the null hypothesis for both series at the 1% level of significance of the (AESTAR) model of Sollis.

The test of Kılıç rejects the null hypothesis at the 5% level of significance for only the detrended data of both series. When demeaned data was used, the null of unit root test of Kılıç was rejected for only the official exchange rate and at the 10% level of significance. The test of
Kılıç hence provides stronger empirical support for nonlinear stationarity of the official exchange rate compared to parallel exchange rate. Non-linearity in the official exchange rates may rise, as suggested by Bahmani-Oskooee et al [42], from structural breaks due to official devaluation, besides frequent official interventions.

We note that Kılıç, which associates nonlinearity with the size of real exchange rate appreciation or depreciation, provided less evidence in favor of PPP compared to Kapetanios et al and Kruse, which allow for nonlinearity driven by the size of deviations from PPP.  This finding contrasts with that of Yıldırım who found that the strongest evidence for PPP in Turkey is obtained through the unit root test of Kılıç [9].

DISCUSSION

Transaction costs and trade barriers are the plausible sources of nonlinearity in real exchange rates during the period of the study. It is important to note that the imposition of financial and economic sanctions has restricted exports and imports in Syria. (These sanctions include the freezing of Government of Syria assets, the cessation of transactions with individuals and companies in Syria, the termination of all investments supported by foreign Governments and the banning imports of Syrian oil). Indeed, the great government spending on nontraded goods compared to traded goods during the period of crisis has increased the share of nontraded goods.

The nonlinearity of exchange rate series may also arise from frequent official interventions in the foreign exchange market. In fact, the continuous deterioration in the economic fundamentals, in addition to the speculative pressure and the capital flight have contributed to sharp depreciation of the Syrian pound during the period of crisis, which authority tried to counter through increasing the interventions. These interventions could lead to non-linearity into the adjustment of the nominal exchange rate and, with price stickiness in the short run, the adjustment of the real exchange rate as well [1,42]. Note that, as stated in Dutta and Leon [43], policymakers in less developed countries prefer having longer periods of currency appreciation than depreciation, even though the economic fundamentals would require the opposite. This could be explained by fear of inflation (pass-through from exchange rate swings to inflation) and currency mismatches.

The high level of inflation could be another possible contributor to adjustment of real exchange rates series. The annual inflation rate in Syria reached 163.1% in December 2020 compared to the base year 2010, the year before the eruption of the Syrian crisis [44]. This implies, as argued by Cashin and Mcdermott [34], more frequent adjustment of goods prices, which could reduce the duration of deviation from PPP. Note that as prices have less of a tendency to move downwards, the exchange rate might have to do more of the adjusting. An adjustment might thus be asymmetric between the upward and downward deviations from equilibrium [38].

Our results can also provide some evidence on how the monetary authority in Syria reacted in the period of crisis. According to IFM reports, the exchange rate classification of Syria was changed from “stabilized arrangement” to “other managed management” on April 2011, in the aftermath of the crisis that erupted on March 2011 [37]. This means moving to more flexible exchange rate regime. In 2012, the prime minister issued the law No. 1131 which stated the movement towards a free exchange rate regime, with the right of the Central Bank of Syria to intervene in the exchange market to correct the exchange rate trends in the market. We believe that moving to a more market-oriented exchange rate has facilitated the nominal exchange rate adjustment. As discussed in Cashin and Mcdermott [34], more flexibility in nominal exchange rates may increase the speed of the parity reversion of real exchange rates by encouraging more frequent adjustment of goods prices. These findings are consistent with those of Baharumshah et al, as they found that the weak form of PPP holds for six East-Asian countries only over the post-crisis period [45]. They suggest that the evidence in favor of PPP was stronger following the financial crisis when countries had to abandon pegging their exchange rates. We also believe that interventions in the foreign exchange market have some justification as the deviations of real exchange rates from the equilibrium appear to be temporary and the exchange rates are adjustable towards PPP.

CONCLUSION AND RECOMMENDATION

This study investigates the PPP hypothesis for Syria over the period (2011:04-2020:08), using both official and parallel real exchange rates of the Syrian Pound against the US Dollar. To this end, a battery of nonlinear unit root tests is adopted along with popular conventional unit root tests.

The conventional tests (ADF and PP) fail to reject the null of a unit root for the real exchange rate series at the 5% level of significance, regardless of whether we use official or parallel exchange rate. The non-stationarity of both series is robust to the existence of breaks since the Lee and Strazicich unit root tests fail to reject the null hypothesis at the 5% level of significance for both official and parallel series.

When nonlinearity is incorporated in the testing procedure, the nonlinear tests of Kapetanios et al, Kruse, and Sollis support PPP for both real exchange rate series under consideration at the 1% level of significance. The test of Kılıç supports PPP only after allowing for a trend in both series and at the 5% level of significance.

The findings of this study provide new evidence on the behavior of exchange rates in Syria during the recent period of crisis. The non-linear mean reversion indicates that as the real exchange rate deviates from its long-run equilibrium, it tends to have faster speed of adjustment. This implies that PPP can be used to determine whether the currency is overvalued or undervalued, and investors and speculators are not able to obtain unbounded gains from arbitrage [9,45].

Finally, as our results signify the importance of non-linear adjustment in real exchange rates, it is so important that policymakers and exchange rate market participants take account of possibility of nonlinear dynamics in their decisions. Future research should also take on the issue of nonlinearity of real exchange rate more seriously when examining the PPP.

 

References :
  1. Sarno L., Taylor M.P. Purchasing power parity and the real exchange rate. IMF Staff Pap. 49, pp.65-105; 2002.
  2. Hegwood N.D., Papell D.H. Quasi purchasing power parity. Int. J. Financ. Econ, Vol.3 No.4, pp.279-289; 1998.
  3. Perron P. The great crash, the oil price shock and the unit root hypothesis. Econometrica 57, pp.1361-1401; 1989.
  4. Zivot E., Andrews D.W.K. Further evidence on the great crash, the oil-price shock, and the unit-root hypothesis. J. Bus. Econ. Stat. 10, pp.251-270; 1992.
  5. Lumsdaine R.L., Papell D.H. Multiple trends breaks and the unit root hypothesis. Rev. Econ. Stat. 79, pp.212-218; 1997.
  6. Lee J., Strazicich M.C. Minimum Lagrange multiplier unit root test with two structural breaks. Review of Economics and Statistics 85, pp.1082-1089; 2003.
  7. Lee J., Strazicich M.C. Minimum LM unit root test with one structural break. Working Paper, Department of Economics, Appalachain State University; 2004.
  8. Taylor M.P., Sarno L. The behaviour of real exchange rates during the post Bretton Woods period. J. Int. Econ. Vol.46, pp.281-312; 1998.
  9. Yıldırım D. Empirical investigation of purchasing power parity for Turkey: Evidence from recent nonlinear unit root tests. Central Bank Review 17, pp.39-45; 2017.
  10. Rogoff R. The purchasing power parity puzzle. J. Econ. Lit. Vol. 34, pp.647-668; 1996.
  11. Dumas B. Dynamic equilibrium and the real exchange rate in spatially separated world. Rev. Financ. Stud. 5, pp.153-180; 1992.
  12. Sercu P., Uppal R., Van Hulle J. The exchange rate in the presence of transactions costs: implications for tests of purchasing power parity. J. Financ. 50, pp.1309-1319; 1995.
  13. Obstfeld M., Taylor A. Nonlinear aspects of goods-market arbitrage and adjustment: Heckscher’s commodity points revisited. Journal of the Japanese and International Economies, Vol. 11, p. 441-479; 1997.
  14. Enders W., Granger C.W.J. Unit root tests and asymmetric adjustment with an example using the term structure of interest rates. Journal of Business and Economics Statistics 16, pp.304–311; 1998.
  15. Caner M., Hansen B. Threshold autoregression with a unit root, Econometrica, Vol.69 No.6, pp.1555-1596; 2001.
  16. Kapetanios G., Shin Y., Snell A. Testing for a unit root in the nonlinear STAR J. Econ. 112, pp.359-379; 2003.
  17. Taylor A.M., Peel D.A., Sarno L. Nonlinear mean-reversion in real exchange rates: toward a solution to the purchasing power parity puzzle. Int. Econ. Rev., Vol. 42, pp.1015–1042; 2001.
  18. Christopoulos D. K., Leon-Ledesma M. A. Smooth breaks and non-linear mean reversion: Post-Bretton Woods real exchange rates. Journal of International Money and Finance, Vol. 29 No.6, pp.1076-1093; 2010.
  19. Kruse R. A new unit root test against ESTAR based on a class of modified Stat. Pap. 52, pp.71-85; 2011.
  20. Taylor M.P., Taylor A.M. Purchasing power parity debate. J. Econ. Perspect. Vol.18 No.4, pp.135-158; 2004.
  21. Bahmani-Oskooee M., Gelan A. Testing PPP in the non-linear STAR framework: evidence for Africa. Econ. Bull. Vol.6 No.17, pp.1–15; 2006.
  22. Teräsvirta T. Specification, estimation and evaluation of smooth transition autoregressive models. J. Am. Stat. Assoc. 89, pp.208–218; 1994.
  23. Sollis R. Evidence on purchasing power parity from univariate models: The case of smooth transition trend-stationarity. Journal of Applied Econometrics, Vol.20, pp.79-98; 2005.
  24. Kılıç R. Testing for unit root in a stationary ESTAR processs”. Econ. Rev., Vol. 30 No.3, pp.274-302; 2011.
  25. Sollis R. A simple unit root test against asymmetric STAR nonlinearity with an application to real exchange rates in Nordic countries. Econ. Model, Vol.26, pp.118–125; 2009.
  26. Kilian L., Taylor M.P. Why is it so difficult to beat the random walk forecast of exchange rates? Journal of International Economics, Vol. 60 No. 1, pp. 85-107; 2003.
  27. Chortareas G., Kapetanios G. The Yen real exchange rate may be stationary after all: evidence from nonlinear unit root tests. Oxf. Bull. Econ. Stat. 66, pp.113-131; 2004.
  28. Narayan P. K., Narayan S. Are real exchange rates nonlinear with a unit root? Evidence on PPP for Italy: A Note. Applied Economics, Vol.39 No.19, pp.2483-2488; 2007.
  29. Bahmani-Oskooee M., Kutan. A. M., Zhou S. Towards solving the PPP puzzle: Evidence from 113 countries. Applied Economics. Vol.41 No.24, pp.3057-3066; 2009.
  30. Vasconcelos C.R., Júnior L.A. Validity of purchasing power parity for selected Latin American countries: Linear and non-linear unit root test. Economia 17, pp.114–125; 2016.
  31. Nazlioglu S., Altuntas M., Kilic K., Kucukkkaplan, I. Purchasing power parity in GIIPS countries: evidence from unit root tests with breaks and non-linearity”. Applied Economic Analysis, Vol.30 No.90, pp.176-195; 2022.
  32. Hassanain K. Purchasing power parity: Further evidence and implications. Review of Middle East Economics and Finance, Vol. 2 No.1, pp.63-77; 2004.
  33. El-Ramly H. Testing for purchasing power parity in a panel of Middle-Eastern Countries. International Business and Economics Research Journal, Vol.4 No.12; 2005.
  34. Cashin P., Mcdermott C. J., Parity reversion in real exchange rates: fast, slow, or not at all? IMF Staff Papers, Vol.53 No.1; 2006.
  35. Kula F., Aslan A., Feridun M. Purchasing power parity in Mena revisited: Empirical evidence in the presence of endogenously determined break points”. Ekonomska Istraživanja, Vol 24 No.1, pp.1-12; 2011.
  36. Al-Ahmad Z., Ismaiel L. Testing the PPP using unit root tests with structural breaks: Evidence from politically unstable Arab countries. International Journal of Business, Economics and Management, Vol.3 No.12; 2016.
  37. International Monetary Fund (2013, 2020), “Annual Report on Exchange Rate Arrangements and Exchange Restrictions”, (USA: International Monetary Fund).
  38. Bahamani-Oskooee M.A., Hegerty S.W. Purchasing power parity in less-developed and transition economies: a review paper. J. Econ. Surv. 23, pp.617–658; 2009.
  39. Taylor A.M. A century of purchasing-power parity. Review of Economics and Statistics, Vol. 84 No. 1, pp. 139-150; 2002.
  40. Abadir K.M., Distaso W. Testing joint hypotheses when one of the alternatives is one-sided. J. Econ. Vol.140 No.2, pp.695-718; 2007.
  41. Broock W.A., Scheinkman J.A., Dechert W.D., LeBaron B. A test for independence based on the correlation dimension. Econometric Reviews, Vol. 15 No. 3, pp.197-235; 1996.
  42. Bahmani-Oskooee. M., Kutanb A.M., Zhou S. Black and official market exchange rates and purchasing power parity: More evidence from non-linear STAR tests. Working Paper; 2006.
  43. Dutta J., Leon H. Dread of depreciation. Measuring real Exchange rate interventions. IMF Working Paper no. 63; 2002.
  44. Inflation reports, Central Bank of Syria.
  45. Baharumshah A.Z., Tze-Haw Ch., Fountas S. Re-examining purchasing power parity for East-Asian currencies: 1976–2002. Applied Financial Economics 18, pp.75–85; 2008.

Fund: No funding is allocated for this work.

Author contributions: The author has contributed all elements of the paper.

Data and materials availability: All data are available in the main text.

 Competing Interests :

The Authors declare that they have no competing interests.

 

(ISSN - Online)

2959-8591

Article Information :

  1. Submitted :16/04/2023
  2. Accepted :13/06/2023

Download

  1. Downlaod Article as Pdf

DOI

  1. 10.5281/zenodo.8253574

Correspondence

  1. linda.ismaiel@tishreen.edu.sy

Cited As

  1. Ismaiel L. Testing the Validity of Purchasing Power Parity for Syria: Evidence from Non-Linear Unit Root Tests. Syrian Journal for Science and Innovation 2023;1. https://doi.org/10.5281/zenodo.8253574.

Current Issue