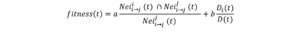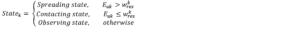A Comparison of Four Information Diffusion Inspired-Based Models According to Real Data Diffusion Similarity
2023-11-27 | Volume 1 Issue 3 - Volume 1 | Research Articles | Amjad Alloush | Ghaida Rebdawi | Mohammad Saeed Abou-TrabAbstract
The rapid revolution in web technology has brought much attention to social media platforms. The main focus was on how information spreads across the network topology. Various information diffusion models have been introduced to study diffusion on social media. However, the inspired-based model is a spark that can more realistically mimic real-world scenarios. In this study, we compared four inspired-based models to flash a glance at (immune-inspired, genetic-based, potential-driven, and particle collision) models in terms of their strengths and limitations. We compared the previously listed models based on their similarity to actual data diffusion. Then, we propose an experiment on these models to show how the Immune-based model is the best for fitting the real data propagation of the introduced models, and how the seed set of the nodes is the primary factor that determines the diffusion paths.
Keywords : Social Networks, Information Diffusion, System-Inspired.
INTRODUCTION
social networks play a crucial role in the dissemination of information. Social media has changed the way people interact with the news. In the past, people only received news and events, while, on the contrary, social networks transformed people into engaged parties by allowing them to create, alter, and spread the news. Currently, many models have been developed to study information dissemination over social networks. The importance of social media in affecting societies has also been considered. The absence of censorship [1] existing in traditional media (magazines and newspapers), makes them promising environment for viral marketing [2], rumor breeding [3], and crowd control by changing their attitudes, brains, and practices. The contribution of this study is the comparison of four new inspired-based models in terms of their similarity with real data diffusion. We focus on this similarity factor because of its importance in social networks. As networks simultaneously reach billions of connected users, the model must comply with good real-data diffusion criteria to be applicable in real-life cases. This paper is organized as follows: In the next section, we discuss elementary diffusion models and some important definitions, and then introduce the four inspired-based models in more detail to show their capabilities. Next, we present and compare the experimental dataset used to test these models. Finally, we discuss the findings and suggest future work. Our research tries to answer the following question: in terms of performance of the four information diffusion models, which one is the most suited for real data diffusion? This aim reflects the goals of the study in comparing different information diffusion models and assessing their performance against real data, which can be valuable for both academic research and practical applications.
MATERIALS AND METHODS
Elementary Models and Definitions
In this section, we discuss the basic models of diffusion and the basic terms used in the remainder of this study. Social networks [4] are intended to disseminate innovations. Kempe et al. [5] are the first who model Influence Maximization (IM) through social networks. In this study, Kempe presented an analysis framework that is meant to be the first approximation guarantee for an efficient algorithm to select the most influential node-set. This framework uses the nature of greedy algorithm strategies to obtain a solution that is 63% suitable for the most basic models. Influence maximization [4] could be defined by selecting a seed set of nodes where the network reaches the maximum influence according to this set. The target of any influence model is to maximize influence and predict how information dissemination paths can be obtained.
Models Representations
A diffusion model represents the social network as a graph G = (V, E), where G is the graph or network, V represents the vertices that model the users in the networks, and E contains the edges that represent the relation or interaction between users in the corresponding social networks. Many diffusion models have been proposed to mimic information dissemination. Li et al. [6] categorized the models into two categories: progressive diffusion models and non-progressive models. In Progressive diffusion models, nodes that are activated or infected by other nodes cannot be recovered or deactivated from the dissemination propagation. Linear Threshold (LT) and Independent Cascade (IC) are examples of these models. Linear Threshold (LT) and Independent Cascade (IC) models are the primary models. LT [7] is defined by Granovetter as a node that can be in one of two states (active/inactive) and can be turned from active to inactive based on the activation function, which is the sum of the weights of the neighbor nodes. If the sum exceeds the threshold, then the node turns on active and starts the diffusion process. If the node is not activated on the first attempt, it will remain inactive on the next attempt. The IC model [8] is more likely to be LT, but the activation function is based on statistical probability to determine whether the node will be active when propagation starts or whether it will remain inactive. In non-progressive diffusion models, the node might be deactivated after some time of activation and stop propagating the diffusion. Examples of non-progressive diffusion models are typical epidemic disease models like the Voter model [6] and the Susceptible-Infected (SI) model [9] and their ancestor’s models Susceptible-Infected-Susceptible (SIS) [9] and Susceptible-Infected-Recovered (SIR). Kermack at al. proposed the Susceptible-Infected-Recovery (SIR) model [10], which is an epidemical model that considers the population as constant, while the nodes could fall into one of three modes: Susceptible where the node can get infected by the disease, Infected where the node is infected by the disease and Recovered where the node has recovered from the disease and will not get infected again. The basic models mentioned above were used in all proposed models.
Related Works
Experiments conducted with actual real-world data have played a crucial role in evaluating the effectiveness and practicality of diffusion models. These investigations highlight the importance of testing models under lifelike conditions, offering valuable insights into the intricate nature of information spread across different situations. Several noteworthy contributions that have enhanced our comprehension in this regard encompass: Ugander et al. [11] in their influential study, examined the diffusion of information within the Facebook network. By analyzing the spread of content such as news articles and videos, they compared the observed diffusion patterns with predictions from various models. This work revealed the nuances of information flow within an online social network, shedding light on the models’ capabilities and limitations in capturing real-world dynamics. Myers et al. [12] explored the retweeting behavior on Twitter, focusing on how information spreads through the network. By investigating the viral diffusion of tweets and memes, they provided insights into the role of influential users and the temporal dynamics of retweets. This study highlighted the need for temporal considerations in diffusion models and emphasized the significance of early adopters. González-Bailón et al. [13] Investigating the diffusion of content across the blogosphere, he examined the interplay between the content’s virality and the network structure. They found that diverse and well-connected blogs are more likely to spread information widely. This study showcased how the characteristics of the dissemination platform interact with the content itself to influence diffusion patterns. Bakshy et al. [14] studied the diffusion of news articles on Facebook, revealing the role of social influence and algorithmic curation in shaping the visibility and spread of content. They found that exposure to friends’ interactions with news stories significantly influenced users’ engagement. This work highlighted the interplay between social connections and platform algorithms in information diffusion. Weng et al. [15] conducted a comprehensive comparison of different information diffusion models using Twitter data. By analyzing the spread of hashtags, they evaluated the performance of models like Independent Cascade and Linear Threshold in predicting real-world diffusion. This study contributed to the understanding of how different models approximate observed diffusion patterns. Building upon the traditional models, Liu et al. [16] introduced a dynamic variation, the Time-Critical Diffusion Model, which incorporated temporal factors for predicting information spread. Their work highlighted the temporal aspect as a crucial component of diffusion modeling, especially in scenarios where the urgency and timing of information propagation play a critical role. Smith et al. [17] conducted an empirical study comparing several diffusion models on real-world social network data. Their findings revealed that the performance of models varied significantly depending on the characteristics of the network and the nature of the information being propagated. Additionally, Kumar et al. [18] introduced a new model called the modified forest fire model (MFF). Their work is based on the enhancement of an existing model and the introduction of the term ‘burnt’ to represent nodes that stop propagating information. They used real Twitter datasets to compare their model with the SIR and IC basic models to demonstrate the feasibility of their work.
Theory/Calculation
Many studies have focused on models inspired [1, 19-21] by physics, sociology, mathematics, and so on. In addition, optimizations can be obtained from these inspiration-based models to solve complex computational issues using swarm-based intelligence or to mimic natural phenomena to solve optimization problems.
Diffusion Models
In this study, we focus on four different inspired-based models to demonstrate their ability and the limitations that need to be addressed in future research. These models were selected based on their popularity and the publication dates of their research. Similarity to the diffusion of real data appears to be the most important comparison feature when dealing with social networks. Predicting the diffusion paths of any post or tweet can help in predicting its consequences and effects, the data provenance of rumors after rumor diffusion, or sources of fake news. Table 1 provides a short description of each of the four models.
Immune System-Inspired Information Diffusion Model
The Immune System-Inspired information diffusion model proposed by Liu et al. [21], mimics the immune system of the human body. The human immune system attempts to handle and eliminate non-self-material by recognizing microbes and studying their information to decide the best way to deal with them. However, immunity deals with antigens in different ways, using memory to prepare for action, either leaving or trying to eliminate them. This biological structure of immunity resembles the information diffusion process, where antigens represent the information received by users, and antibodies represent the users who receive the information. User responses to information vary from one user to another according to their immune system, which is represented by the fitness function. The fitness function could be formulated according to Liu [21] as
Where and represents the neighbors of node I and j in time t, when the information is disseminated, respectively. The equation represents the common friends of the node and at time . represents the degree of an entire network while the is the degree of node . and are weighted variables determined by the network structure. The calculation of the fitness function determines whether the value exceeds the activation threshold to start diffusion or is below the threshold to keep the information on the immune list, where it will be ignored. The immune list retains this information as a long-lasting memory to keep discarding it when the body receives it again. Diffusion between persons is not constant, as in other non-inspired models, but it is a dynamic diffusion that varies from one person to another. One of the greatest limitations of this model is that it considers time. Time progress increases the immunity of the nodes and decreases the diffusion process. In addition, this model assumes that all the nodes are simultaneously active, which is not the case in reality. Moreover, this model does not consider the content of the information, which is a critical aspect of diffusion. Different information expressions lead to different diffusion paths. However, this was not considered in the model. This model must find the most influential node with a high degree of connection to accelerate diffusion. The saturation of diffusion of a single node leads this node to lower its immunity and propagate the information forward.
Genetics-Based Diffusion Model
The Genetics-Based diffusion model was proposed by Li et al. [20]. The idea behind this model is to use a genetic algorithm (GA) to mimic the diffusion process in social networks. The chromosomes represent the nodes, and the gene represents the message. This model was built on top of the epidemic-spread susceptible-infection model. The main objective of this model is to spread multiple objects with different relationships across various social media platforms despite the other spreading models. The process of this model starts with crossover when the genetic algorithm begins, and the new gene contains the information that will spread across the network. The cross-over may lead to a split of the information which is called information loss. However, this problem is solved by comparing the content of the old genes with that of the new ones to ensure that the information is preserved. The breakpoint is the term meaning that the spread starts slowly until it reaches this point; then, the spread starts increasing rapidly. The computational cost [12] of this algorithm is low, because it’s depending on the directed graph where information is passed from the sender to recipients. This imposes to take action if the diffusion must be stopped before reaching this point. A weakness of the proposed model appears when only one message that spreads the information behaves exactly like the way in the Susceptible-infected (SI) model; the model failure appears [12] when attempting to spread two contradictory pieces of information as the experiment done by Li, which ends with slowing propagation and making its result unpredictable. The experiment yielded different results when conducted using two independent messages. Therefore, the behavior of this model did not proceed as expected. The best performance appears with dependent information.
Particle-Model of Diffusion
The particle model is inspired by the elastic and inelastic collisions of particles. It is presented by Xia et al. [1]. It is based on the particle collision system, where the influence of diffusion is represented by the kinetic energy obtained from the particle collisions, while the user influence is represented by the particle mass. Xia represents this model on a smooth surface to represent the particle collisions on the damping orbit. He [1] formulated a model as follows: the user should be considered a mass particle. After a collision in orbit, the user can be in one of three states:
Where: represents the energy particle k obtained from after the collision. represents the energy particle k needs to pass the damping track. When the particle has the energy to pass through the damping orbit, it hits other particles and spreads information. The particle stops at the damping track when it has no energy to continue colliding with other particles, so the particle will be in a contracting state. Otherwise, the particle will never collide with the other particles, which represents the user in the inactive mode. The primary feature of this model is to highlight the user’s perspective in information diffusion, where the user’s influence plays a crucial role in the process. This model is based on the Susceptible-infected (SI) model. This model can work with a big network according to the proposed article where he could deal with millions of spreaders and larger networks [1]. The weakness of this model is that it varies depending on the initial set that determines its ability to diffuse. Diffusion starts slowly and then grows rapidly with time, and collision continues.
Potential-Driven Diffusion Model
The last model is the Potential-Driven Model, it is proposed by Felfli et al. [19]. This model takes advantage of a physically inspired approach. The nodes were represented as particles. The relationship between nodes is represented by the forces between particles. Each particle creates a potential at its location, which determines the influence of forces between nodes in the graph. The proposed architecture can yield good results compared with greedy algorithms, which are used to calculate the seed set to achieve influence maximization (IM) in the network; however, the computational cost of calculating this set is high, to determine the potentials for individual nodes, the net potential algorithm exhibits [19] a computational complexity of O(n2), where n represents the network’s size, specifically the number of nodes it comprises. The most resource-intensive step within this process is the calculation of pairwise distances (RSP), as it necessitates the inversion of an n x n square matrix, giving rise to a computational complexity of O(n3), which limits this approach to small networks and makes it infeasible for large networks. The researcher limits the samples of their networks during the experiments to be varying from 250 to 100,000 nodes, because of its highly computational cost. In addition, the features of timestamp, location, topic, and feel add complexity to the selection of seed nodes. This model [19] attempts to use the simulation-based approach or the sketch-based approach. The simulation-based approach variation is based on a greedy algorithm and Monte Carlo simulation. The sketch-based approach avoids using the extensive Monte Carlo calculation by using grounded sketches under the dissemination model. The most important feature of the potential-driven model is its ability to mimic the influence between nodes, such as forces between nodes. It uses an approximation to calculate the influence score of the entire network by considering this network as a closed static system of particles. This model is considered an extension of the linear threshold model. Static networks are considered one of the biggest limitations of this model. Tables (2 and 3) presents consecutively the pros and cons of the models mentioned above.
Experiment:
Selecting the diffusion model to be used in any case depends on several factors. These factors vary depending on the model’s capabilities for adapting to large networks, dynamic networks, and similarity to real data diffusion paths. The resemblance between the selected model and real diffusion offers a great opportunity for responsible parties to predict the results and consequences of the diffusion of any posted information on society.
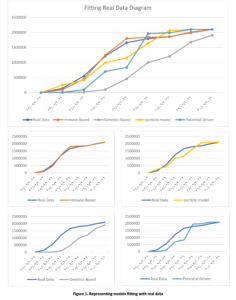
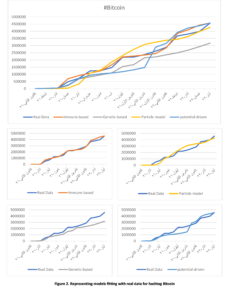
In fake news spreading, the model provides the ability to trace the information after starting the diffusion to locate the false news spreader and take appropriate action to stop the dissemination. We applied the previously listed models to determine which one best fit the real data. We selected a hot topic that has recently arisen, “death of people after boat sinks off”. This information first appeared on Thursday September 22, 2022. We collected 2.1 million blogs from 22nd September to 30th September, then we counted the users who discussed this topic. The data collected using the twitter API development by selecting the trends and collected the users and data. The data collected by help from https://www.kaggle.com where the researchers could ask them to collect a data-set. Furthermore, we utilized a data-set sourced from the Twitter social network [22], specifically related to the hashtag #Bitcoin. Bitcoin, a decentralized digital currency commonly known as a cryptocurrency, was introduced in 2009 by an individual or group using the pseudonym Satoshi Nakamoto. The dataset encompasses tweets extracted from the period of January 21, 2021, to May 31, 2022, comprising approximately 4,569,721 tweets. In the experiment, we used the set of users who first posted the information on the first day as a seed set (initial value for node activation), and we implemented the four previous models on this data to find the best model for both data-set. The x-axis represents time, and the y-axis represents the number of engaged users in the dissemination of information over time. The similarity of the previous model with real data is shown in Fig.1. and Fig.2.
RESULTS
The findings of our research paper shed light on the performance and effectiveness of four different diffusion models: the Genetic-based Model, Potential-driven Model, Particle Model, and the Immune-based Model. Each model was subjected to rigorous experimentation and evaluation against real-world diffusion data to understand their strengths and limitations in accurately representing information dissemination dynamics in networks.
EXPERIMENT METHODOLOGY
- Selection of Diffusion Models: We selected four different diffusion models, each presumably designed to represent the spread of information in networks in a unique way. These models are the Genetic-based Model, Potential-driven Model, Particle Model, and the Immune-based Model.
- Collection and Analysis of Real-world Diffusion Data: we collected real-world diffusion data, which likely includes data on how information (death of people) or trends (Bitcoin) spread through networks. This data serves as the basis for evaluating the performance of the diffusion models.
- Data Preparation: The real-world diffusion data was likely cleaned and prepared for analysis to ensure its accuracy and relevance.
- Model Implementation: Each of the four diffusion models was implemented or simulated based on their respective algorithms and methodologies.
- Comparison and Evaluation: The performance of each model was evaluated by comparing its predictions or simulations with the actual diffusion data.
- Strengths and Limitations Assessment: As part of the evaluation, our aim was to understand the strengths and limitations of each diffusion model. This would involve identifying where each model excelled and where it fell short in accurately representing the dynamics of information dissemination.
DISCUSSIONS
Genetic-based Model: The Genetic-based Model exhibits a slow diffusion process initially, characterized by a gradual increase in the spread of information. However, it undergoes a turning point where the diffusion rate rapidly accelerates, leading to a swift dissemination of information throughout the network. While this high rhythm in the later stages might seem promising, it fails to align well with the actual diffusion data. The model’s behavior deviates significantly from the observed real-world diffusion patterns, making it less suitable for capturing the intricacies of information propagation in networks. This model suffers from the overfitting, when the model is trained, it learns to fit the training data as closely as possible, aiming to minimize errors and discrepancies between the model’s predictions and the actual data points. However, overfitting occurs when the model becomes too specialized in capturing the noise and intricacies present in the training data, rather than learning the underlying patterns or relationships.
Potential-driven Model: In contrast to the Genetic-based Model, the Potential-driven Model does not fit well with the real diffusion process at the outset. In the early stages of diffusion, the model exhibits discrepancies with the actual data, indicating its limited accuracy in capturing the initial spread of information. However, as the diffusion progresses towards its final stages, the Potential-driven Model starts to converge and better matches the real data. This suggests that the model’s performance improves in the later stages of diffusion, but it may not be the most reliable choice for predicting the early stages of information dissemination. This model is designed to work over Static networks where they refer to networks that do not account for the dynamic nature of relationships and interactions in real-world social networks. In reality, social networks are often highly dynamic, with relationships forming, evolving, and dissolving over time. This static representation can oversimplify the complex, evolving nature of real social networks.
Particle Model: The Particle Model demonstrates some resemblance to real diffusion, showcasing numerous conversions observed in the experiment across various diffusion paths. This indicates that the model is capable of capturing some essential aspects of information propagation in networks. However, it falls short in accurately representing the complete diffusion process, as there are still notable disparities between the model’s behavior and the observed real-world diffusion dynamics. The identified problem of this particular model lies in its sensitivity to the initial set, a factor that significantly impacts its diffusion characteristics. When the model is initiated with different sets of conditions or parameters, it exhibits varying behavior, thereby influencing its effectiveness in spreading information or influence throughout the network.
Immune-based Model: Among all the models tested, the Immune-based Model stands out as the best fit for the real diffusion process. It showcases remarkable accuracy in mimicking the spread of information across networks, consistently aligning with the observed real-world diffusion patterns. The Immune-based Model’s success is attributed to its adaptive learning mechanism, inspired by the human immune system, which enables it to identify and target influential nodes in the network effectively. This adaptive behavior allows the model to make precise predictions and accurately capture the complex dynamics of information dissemination in various network structures. In conclusion, the Immune-based Model emerges as the most promising candidate among the tested models for modeling information dissemination dynamics in networks accurately. Its ability to adaptively learn and replicate real-world diffusion processes positions it as a valuable tool for various applications, such as social media analysis, viral marketing campaigns, and epidemic spread prediction. These findings contribute to the advancement of research in network information propagation and provide essential insights for developing effective strategies to influence and control information flow in interconnected societies. However, further investigations and refinements of the other models may offer valuable insights into their potential applications in specific scenarios and provide a comprehensive understanding of their strengths and limitations.
CONCLUSIONS
The primary aim of this study was to conduct a comparative analysis of various inspired-based diffusion models. Four distinct models, namely immune-inspired, genetic-based, potential-driven, and particle collision, were evaluated based on their similarity to the diffusion patterns observed in real social networks. Through meticulous experimentation and analysis, the study conclusively determined that the immune-based diffusion model exhibited the closest fit to the actual information dissemination in social media applications.
RECOMMENDATIONS
As we move forward, future research endeavors should seek to capitalize on the strengths of each of the aforementioned models. By integrating the best aspects of these models, researchers can strive to develop a more comprehensive and refined diffusion model that is exceptionally well-suited for real-life scenarios. Moreover, addressing the performance bottleneck becomes crucial, with time emerging as a pivotal factor when dealing with the rapid spread of rumors across social media platforms. In summary, the ultimate goal is to design an enhanced diffusion model that not only accurately captures the intricacies of information propagation in social networks but also efficiently addresses the time-sensitive nature of handling misinformation and rumors on these platforms. By achieving this, we can significantly contribute to the advancement of strategies to combat misinformation and uphold the integrity of information shared through social media channels.
References :- Xia Z, Tan Z, Zhang Y, Zhang S, Ma Y. A novel information diffusion model inspired by particle-collision dynamics for online social networks. Proc – 2019 IEEE Intl Conf Parallel Distrib Process with Appl Big Data Cloud Comput Sustain Comput Commun Soc Comput Networking, ISPA/BDCloud/SustainCom/SocialCom 2019. 2019;1629–34.
- C, Rebeca San Jos´e. Social and attitudinal de-terminants of viral marketing dynamics[J]. Computers in Human Behavior, 2011, 27(6):2292-2300.
- Lin D, Lv Y, Cao D. Rumor diffusion purpose analysis from social attribute to social content. Proc 2015 Int Conf Asian Lang Process IALP 2015. 2016;107–10.
- Wan P, Wang X, Wang X, Wang L, Lin Y, Zhao W. Intervening Coupling Diffusion of Competitive In-formation in Online Social Networks. IEEE Trans Knowl Data Eng. 2021;33(6):2548–59.
- Kempe D, Kleinberg J, Tardos É. Maximizing the spread of influence through a social network. Theo-ry Comput. 2015;11:105–47.
- Li Y, Fan J, Wang Y, Tan KL. Influence Maximiza-tion on Social Graphs: A Survey. IEEE Trans Knowl Data Eng. 2018;30(10):1852–72.
- Granovetter, Threshold Models of Collective Behavior, Am. J. Sociol. 83 (1978) 1420–1443.
- Li D, Liu J, Modeling Influence Diffusion over Signed Social Networks, IEEE Trans. Knowl. Data Eng. 33 (2021) 613–625.
- Sumith N. Open RnSIR model for Information Spread in Social Networks. 2020 11th Int Conf Comput Commun Netw Technol ICCCNT 2020. 2020;
- Petard H. A Contribution to the Mathematical The-ory of Big Game Hunting. Am Math Mon. 1938;45(7):446.
- Ugander, J., Backstrom, L., Marlow, C., & Kleinberg, J. (2012). Structural diversity in social contagion. Proceedings of the National Academy of Sciences, 109(16), 5962-5966.
- Myers, S. A., Zhu, C., & Leskovec, J. (2012). Information diffusion and external influence in networks. In Proceedings of the 18th ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 33-41).
- González-Bailón, S., Borge-Holthoefer, J., Rivero, A., & Moreno, Y. (2012). The dynamics of protest recruitment through an online network. Scientific Reports, 2, 594.
- Bakshy, E., Rosenn, I., Marlow, C., & Adamic, L. (2012). The role of social networks in information diffusion. In Proceedings of the 21st international conference on World Wide Web (pp. 519-528).
- Weng, L., Menczer, F., & Ahn, Y. Y. (2013). Virality prediction and community structure in social networks. Scientific Reports, 3, 2522.
- Liu, Y., Gao, H., Du, J., & Zhang, X. (2014). Understanding and modeling the popularity, stickiness, and impact of online content. IEEE Transactions on Multimedia, 16(2), 501-514
- Smith, S. M., O’Connor, B., & Littman, M. L. (2019). Detecting early-stage rumor cascades in social media. In Proceedings of the International Conference on Machine Learning (ICML) (pp. 5987-5995).
- Kumar S, Saini M, Goel M, Panda BS. Modeling information diffusion in online social networks using a modified forest-fire model. J Intell Inf Syst. 2021;56(2):355–77.
- Felfli Z, George R, Shujaee K, Kerwat M. Potential-driven model for influence maximization in social networks. IEEE Access. 2020;8:189786–95.
- Li L, Li S, Chen X. A new genetics-based diffusion model for social networks. Proc 2011 Int Conf Comput Asp Soc Networks, CASoN’11. 2011;76–81.
- Liu Y, Ding Y, Hao K, Chen L. An immune system-inspired information diffusion model. Chinese Con-trol Conf CCC. 2017;11238–43.
- https://www.kaggle.com/datasets/kaushiksuresh147/bitcoin-tweetsAuthor contributions: the author has contributed all elements of the paper.
The Authors declare that they have no competing interests.
Funding: No Fund
Author Contributions: Writing: Amjad Alloush
Supervision – Review: Ghaida Rebdawi, Mohammad Saeed Abu-Trab
Data and materials availability: All data are available in the main text.
(ISSN - Online)
2959-8591