Scientists Had a Groundbreaking Conversation with a Humpback Whale in Her Own Language and It Could Help Humans Chat with Aliens One Day




The importance of investing in knowledge is particularly evident in countries whose natural resources have been depleted because of many reasons. The role of the intellectual capital it possesses is clear, capable of compensating for these material losses through its knowledge products. This clearly applies to the Syrian situation, after more than a decade of military, political and economic wars. It is self-evident that investing in knowledge leads to improvements in technology, efficiency, productivity and economic growth, and paves the way for knowledge transformation in various sectors of the country through research, scientific development and innovation activities. I will here highlight once again the importance of knowledge and technology transfer system that the higher Commission for Scientific Research (HCSR) recently led the work to establish. The system consists of three components; the first component is the technology transfer offices at universities and research centers. Its main short-term goal is to evaluate research outputs completed at research institutions in terms of their applicability and economic feasibility and stimulate the protection of their intellectual property in coordination with the concerned parties. The second component includes R&D departments at state ministries, and later at affiliated or associated companies and business sector institutions. Its main goal is to review the needs for developing production and service sectors and stimulate the conduct of research that meets those needs. Finally, the two previous components are coordinated by a third component represented by the National Office for Technology Transfer NTTO established at HCSR, which links the entities that generate and invest in knowledge. In fact, the past three months have witnessed a number of activities closely related to the technology transfer system. The most important of which was the workshop organized by HCSR to launch the newly established R&D departments in a number of state ministries. This indeed completed the components of the technology transfer system, the first pillar of which was laid down by HCSR in cooperation with the Economic and Social Commission for Western Asia (ESCWA) in a unique report published back in 2020. In addition, NTTO held two important workshops in cooperation with the Universities of Aleppo and Tishreen on enhancing the investment of the research outputs of university professors and postgraduate students at both universities. The two workshops were accompanied by two exhibitions that included a large number of research outputs in the presence of business sector representatives. HCSR will coordinate to organize similar workshops at various other universities. Because we do not ignore the saying: “Happy endings start with new beginnings”, HCSR recently launched the“Researcher’s Guide to Conducting Developmental Scientific Research”. This guide leads researchers and walks with them step by step in conducting their research, starting from choosing the research idea, passing through the initial plan for the research, and arriving at to its primary document, with a self-evaluation form to measure its importance for development. During its last meeting, The National Technology Transfer Committee NTTC formed at HCSR also approved the report entitled “Guiding Procedures for Protecting and Investing Scientific Research Outputs,” which guides researchers through multiple paths to enhance the investment of their research outputs. We do hope that this recently established technology transfer system will be effective in translating the knowledge enhanced at Syrian universities and research centers into products and outputs that aid in the eagerly needed development.
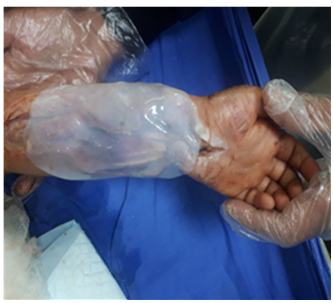
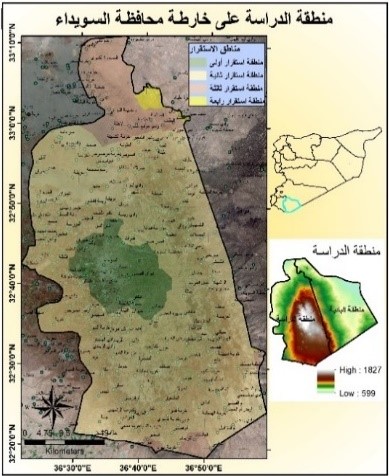
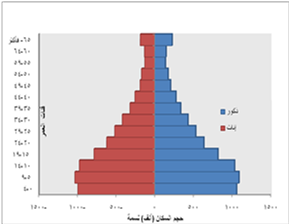



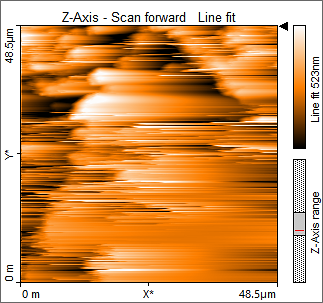
Journal:![]() Syrian Journal for Science and Innovation
Syrian Journal for Science and Innovation
Abbreviation: SJSI
Publisher: Higher Commission for Scientific Research
Address of Publisher: Syria – Damascus – Seven Square
ISSN – Online: 2959-8591
Publishing Frequency: Quartal
Launched Year: 2023
This journal is licensed under a: Creative Commons Attribution 4.0 International License.