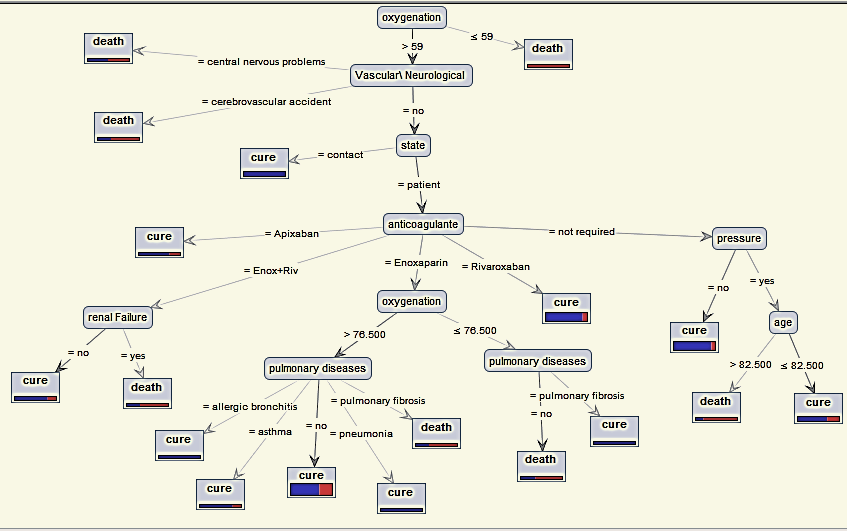
A Classification Process Using Decision Tree Machine Learning Model for Determining the Effect of Anticoagulants on the Fate of Different Types of COVID-19 Patients with Other Diseases


INTRODUCTION
Banning nationally generated certificates that do not have approved global security certificates is a major and fundamental problem in countries that fall under the technical and information ban, such as Iran, Syria, etc., this matter is considered as a paralysis of development wheel in most fields because the aspects of life today have become dependent on electronic transactions, such as: banking sector, electronic transfers and linking them to electronic payment cards, electronic transaction systems, applications that transfer data with a certain degree of confidentiality, custom query systems, web control systems, web ordering systems, all transactions related to electronic government … and other many uses. The root certificate for the root certification authority is issued within a highly protected information environment or system and is used to issue digital certificates to individuals or companies. These certificates and their keys are stored and saved within its private system or environment, and thus the CA is the trusted third party to verify the authenticity of the certificates or signatures that are signed with them. By using the root certificate, verification can be performed, and this is known as the concept of a national certification authority. The National certification authority is considered the cornerstone of everything related to possible applications and projects, including digital transformation, provision of electronic government services (government and civil transactions), electronic payment methods, exchange, approval, authentication and protection of documents, electronic identity, electronic passport, online elections and their integrity, etc. All of these applications or projects depend on the presence of digital certificates signed by the certification authority that issues the digital certificates. Note that these applications or projects require high capabilities to issue digital certificates to all members of the public, as the policy has been adopted in most countries. The National Digital Certification Authority project has not been invested in the optimal way planned for several reasons, the most important of which are: The technological ban on our country, Syria, as the Syrian digital certificate issuing authority is not recognized internationally, and therefore it has not obtained a signature from the global digital certification authorities that are recognized by well-known international browsers. And the inability of well-known international browsers to run applications working on the webs that use nationally generated certificates due to their failure to recognize these certificates because well-known international authentication companies do not certify these national certificates, due to the imposition of technological sanctions on our country and also on many countries that are under the ban. From the above, the need to have a web browser that can verify the authenticity of these certificates in a safe and reliable manner (safety secure way) without the need for authentication from global authorities arose (Certification Authorities). In order to build a web browser that can verify the authenticity of national digital certificates, it requires cooperation between governments and technology companies. Indeed, an agreement had previously been reached between the Network Services Regulatory Authority and a company to build a national web browser, but the project was not completed. In general, it can be said that building a web browser that can verify the authenticity of national digital certificates is necessary to solve the ban problem imposing on certificates, and gives individuals and organizations confidence in using national digital certificates for many purposes. As technology develops and more security technologies become available, this type of browser can be improved and developed to ensure that data security is maintained and authentication is confirmed in a safe and reliable manner, which is an important step in developing and improving the digital infrastructure of countries and individuals, and can help achieve the global goal of maintaining digital security and achieving digital integration between countries, institutions and individuals.
MATERIALS AND METHODS
First, we conducted analytical studies based on field visits to the Ministry of Communications and Technology, the National Authority for Information Technology Services, the government sector, and the private sector to understand the existing problem and discuss it with stakeholders. We also depended on reference studies through books and the Internet about the use of the /SSL, TLS/ protocol in browsers and how this is done through the national digital certificate issuance authority. We followed an inductive research methodology to collect and analyze information, as well as using programming and practical experience to design and develop the national browser. We have depended on a set of programming tools for programming development, which are: Programming by java in Intellij IDE – Programming by java netbeans IDE In addition to a virtual operating system environment on the server VMware Esxi7 (platform virtualization software) Which contains: linuxubuntu server 22.04 operating system. The system for generating digital certificates (Openxpki) wasinstalled, prepared and authenticated, the Windows Server 2022 operating system, where the Wireshark network monitoring tool was installed on it. In order to test the browser’s operation, we used a set of tools: Openxpki which is an open-source tool used globally to generate certificates of all kinds, as it is installed on the Apache web server within the Linux server operating system. A website on which a generated and nationally signed certificate is installed, and Wireshark, a tool used to monitor all network details, including data. The purpose of using it was to indicate whether the connection was successful and the data was encrypted through the https protocol when using national certificates, in addition to national certificates generated and signed by the National Authority for Information Technology Services.
RESULTS
Through this research, we found a solution to the ban problem by creating an open-source software application (web browser), as this browser allows the use of digital certificates approved by the National Authority for Information Technology Services. Other tasks can be added to the browser related to privacy and protection (for example, software code can be added to the browser so that it is linked with a specific web application in order to perform a specific task that may be related to privacy, Property protection, or preventing the use of the application except through this version of the browser…).
DISCUSSION
Description of the X.509 standard:
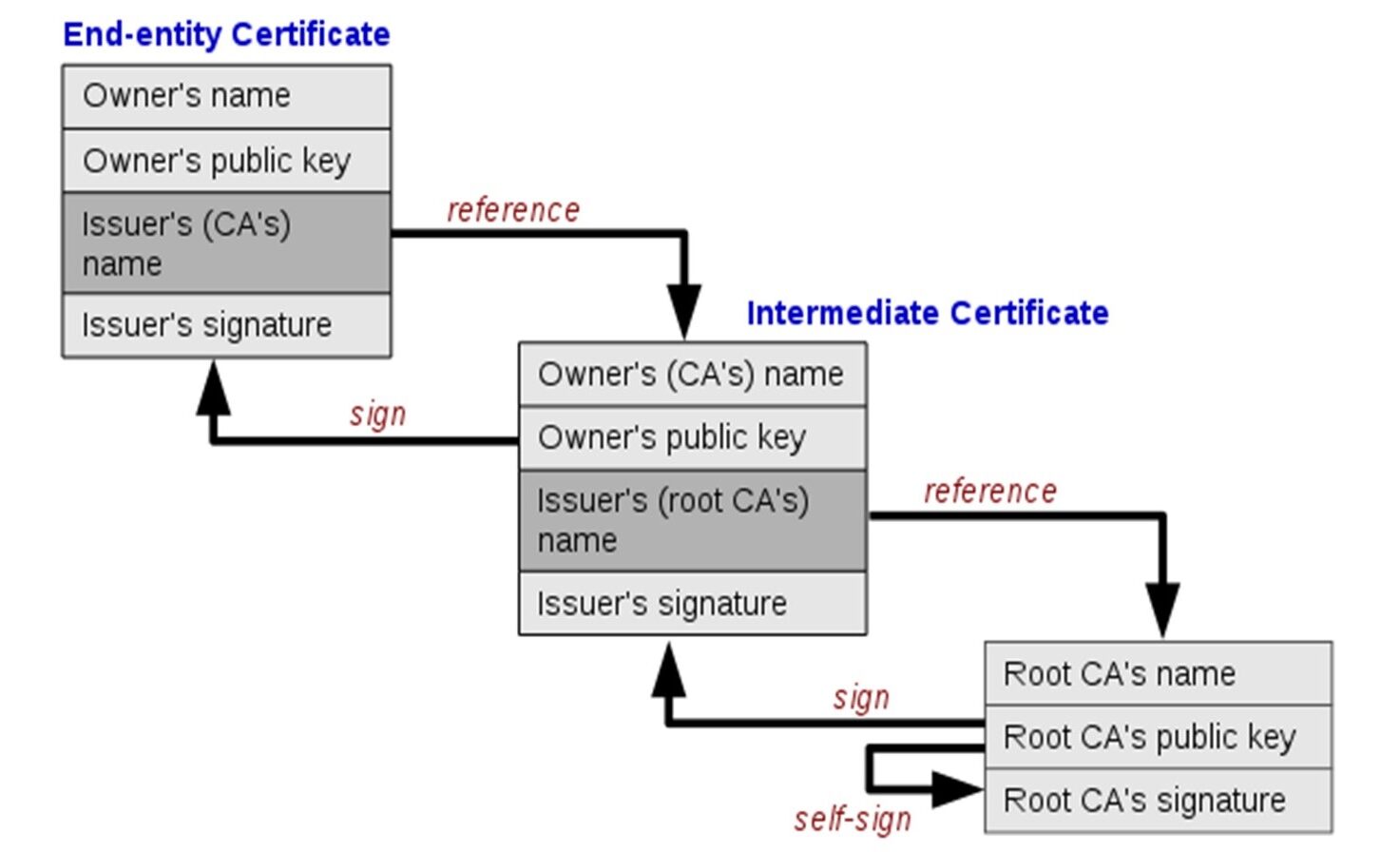
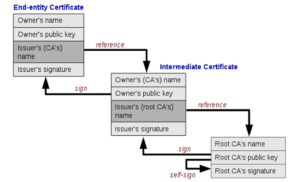
The X.509 standard consists of a set of rules and instructions that determine the method of issuing digital certificates and authenticating digital identity. The X.509 standard is considered the approved reference within the National Digital Certification Authority in Syria. The standard includes detailed information about the entity issuing the certificate and the entity in which the certificate was used, including digital identity information and the keys used in digital signature and encryption. The certifications that depend on X.509 standard are used to authenticate the identity of users, devices, and organizations, by including the digital identity information of the entity issuing the certificate. In general, the X.509 standard forms an important basis for maintaining digital security and authenticating digital identity, as it is used in many different security applications and can be used in many industries and sectors including e-government, e-commerce, banking services, and others. This standard was chosen in our research based on the reference study [1] which confirmed that this standard is used in the majority of global browsers. It analyzed the structure of this standard and how to benefit from it to ensure the identity of servers and the confidentiality of data exchange. The structure of the X.509 standard is illustrated in Figure (3).
Solve the problem by building a national web browser:
A browser was built in the Java programming language that can browse websites using the HTTPS protocol [5]. The browser interfaces were created that resemble the interfaces of well-known international browsers, in addition to building a private trusted certificate store (TrustStore [4]), where trusted certificates are supplied to it through two methods:
Then we tested the readiness of the trusted certificate store. After that, it was adopted as the default store of the national browser instead of the trust store of the operating system. The certificates included in the Trust Store, including the approved nationally generated certificates, can be viewed in Figure (2).
How the browser verifies the validity and reliability of the certificate:
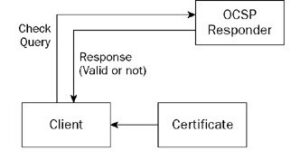
When you browse a secure site (sites that start with the prefix “https://”) instead of “http://”), the browser uses a security protocol called SSL/TLS (Secure Sockets Layer/Transport Layer Security) to secure the connection between the browser and the server [10]. An SSL/TLS certificate is used to authenticate the server’s identity and encrypt the data that is exchanged between the browser and the server. To verify the validity of the certificate, the browser checks the existence of the certificate and whether it was sent by the server. The browser then verifies that the certificate has been signed by a trusted certificate authority (CA) located within the TrustStore [4] that the browser uses, and that the server’s name included in the certificate matches the server’s name in the URL being browsed. Then the browser determines the server’s address of the Online Certificate Status Protocol (OCSP) and the Certificate Revocation List (CRL) server’s address in the digital certificate file that is signed by the certificate issuing institution [10]. The validity of the certificate is checked for revocation or expiration in one of the following two ways:
The OCSP server responds to the request after verifying the validity of the certificate. If the certificate is valid, a positive response is returned confirming its validity, and if it is invalid, a negative response is returned indicating its invalidity. As shown in Figure (4):

By using Certificate Revocation List (CRL), this method includes the following steps:
![Structure of the X.509 standard [researchgate.net]](https://journal.hcsr.gov.sy/wp-content/uploads/2024/03/Structure-300x164.jpg)
OCSP protocol differs from CRL protocol in the following way:
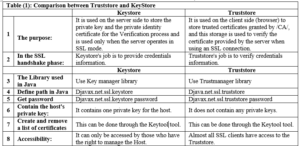
Comparison between the concepts of Keystore and Truststore [4]:
 How to test whether the browser is working properly:
How to test whether the browser is working properly:
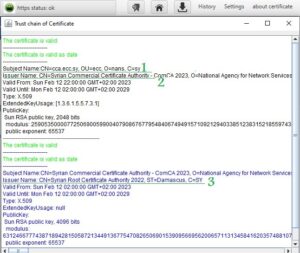
In cooperation with the Digital Certification Center of the National Authority for Information Technology Services within the Ministry of Communications and Technology, an experimental website was developed (https://tools.ecc.sy) on the Internet, embedded with a generated and nationally certified certificate, and its operation was tested on three well-known browsers (MicrosoftEdge، Google Chrome، Mozilla firefox), These browsers were unable to run it due to the existence of the Syrian certificate, which is not trusted by them due to sanctions. The website was tested using the browser that was built and it worked. After running the experimental site on the national browser, the connection was tested if it is secure (encrypted) using the programming code which is custom of testing Https connection. In addition to testing the reliability of the certificate through the browser’s trust store, note that the success of the secure connection is shown by the appearance of a closed lock symbol and writing (Https status: ok) next to the address field within the browser. You can view the certificate for the experimental site described in paragraph 1 above and view the certifying parties (certificate authorities) for this certificate (chain of trust), in Figure (6).
The previous figure shows that the issuer name shown by the number (3) has certified the issuer name shown by the number (2), which in turn has certified the certificate for the experimental site on the Internet shown in number (1). The issuer name (certification authority) shown in the number (1) represents the national Syrian root certificate and is embedded in the browser’s trust store. Accordingly, the experimental site’s certificate was trusted and approved within the HTTPS protocol. When running a site that does not have a certificate or uses the /http/ protocol, the browser will show that. The success of the TLS protocol was monitored through the Wireshark application, which eavesdrops on the entire network. Also monitor data movement (exchanged in encrypted form) across the network through the Wireshark application.
![Verify the certificate through CRL [10].](https://journal.hcsr.gov.sy/wp-content/uploads/2024/03/verify2-300x208.jpg)
CONCLUSION
By the end of the research, the first Syrian national web browser was completed that includes a trusted certificate store that ensures the operation of the https protocol, and offers a set of solutions to the existing problems due to the international technological ban on our country, Syria, and other countries, which prevents us at Syria from using the Internet or the Intranet in the field of reliable electronic dealing in all sectors on government websites which have the SY extension. This Syrian national web browser allows the use of digital certificates approved, generated and signed by the National Authority for Information Technology Services, which are not trusted internationally due to sanctions. Our web browser is a secure, open-source and it can be portable application that does not require installation [2]. Finally, this browser is useful to All entities in the public and private sectors that need to use digital authentication or need protection and reliability in the operation of their applications. In the first place, it will serve the Ministry of Communications and Technology, the National Authority for Information Technology Services in Syria, which presented the National Digital Authentication Project that faltered due to the international browsers not supporting Syrian digital certificates.
FUTURE WORKS
After achieving the desired objectives of the research, which we have mentioned in the context of this article, we can identify a set of recommendations such as: adding tasks related to privacy and protection to the browser, for example adding a digital signature and adding programming code that links the browser to an application for preventing the use of that application except through this version of the browser. The browser can be used as a secure means of communication by adding programming codes that enable communication and the exchange of files and messages. Finally many features can be added and customized when needed for example, adding monitoring features for monitor all types of sites and adding Advanced security and privacy features.
INTRODUCTION
Pollution is a major problem that modern societies suffer from. The presence of pollutants in water resources, especially fresh water, makes it a serious and defining problem for growth and life [1].Pollution issues are constantly exacerbated in Coastal areas because of the increasing of population density and human activities that pollute the environment and natural resources, including water sources and groundwater which represents the reserve stock of water used in various fields [2] Environmental pollution affects all elements of the living environment such as plants, animals and humans, as well as the composition of non-living nature elements such as air, water and land. This problem has exacerbated in recent decades and become a grave danger threatening all living organisms because of industrial development, technological progress, and the development of the human standard of living accompanying with the increasing in consumption and the growing dumping of waste in the environment [3, 4] Solid waste is considered one of the major environmental problems in urban areas, due to its direct impact on the quality of human life, the appearance of civilization, and the consequent serious negative impact on sustainable development [5]. Solid waste resulting from various human activities (production and consumption) has become a major threat to the environment and people because of the increasing quantities generated daily which exceed the ability of the environment to decompose and convert them into useful or harmless materials [4]. The increasing production of raw materials and their consumption contributed to the depletion of natural resources and caused continuous damage to the environment [3]. Every year, the production of raw materials destroys millions of hectares of land and trees and produces billions of tons of solid waste. It pollutes water and air [6], in addition to the pollution resulting from the production and use of energy needed to extract and manufacture materials [7]. Surface water bodies have been used for a long time, and are still used today, as places for discharging various human waste, which exacerbated the problem of fresh water pollution in rivers, lakes and water reservoirs due to a change in its physical, chemical or biological properties. In addition to the pollution caused by these wastes to groundwater when the leachate reaches it [8]. The presence of indiscriminate dumping near water resources (ground or surface) contributes to their pollution and the pollution of the environment in all its aspects, especially groundwater, which represents the reserve stock of water used in various fields affecting growth and life, [9 ,10]. In wet weather, the movement of chemical and biological pollutants of solid waste materials is active, their concentration increases at the bottom of the landfill [11]. Most of leachate coming out of the landfills increases during periods of precipitation. solid waste forms severe pollution sources due to the abundance and diversity of chemical elements emerging from them[12]. Problems with health and environment increase with the appearance of some heavy metals in the groundwater, as specialized references confirm that their presence (no matter how small) is linked to solid waste, as it is one of the most dangerous and toxic chemical pollutants for living organisms [13, 10, 14], and is characterized by its long-term persistence in the aqueous medium, which ranges from several months to several years [14, 15]. The development which Syria witnessed in recent decades has been accompanied by the emergence and exacerbation of environmental pollution problems, as the surface and groundwater in the country suffer from the accelerating rate of bacterial and chemical contamination with industrial, domestic, and fertilizer waste [5]. It has been shown that the pollution, and the amount of waste in general, has increased with the increasing in the population in the countryside and cities, because of the weakness of the treatment plants. [16]. One study also showed an increasing in bacterial population in the water of wells used to irrigate some vegetables near the waste dumping site in the Al-Bassa area in Lattakia during winter [17]. In the same context, the study of the environmental impact of the Al-Bassa landfill [18] concluded that some indicators of contamination of groundwater wells in the Al-Bassa area increased, and it was noted that the rates of BOD and NO3 increased above the permissible levels for drinking water. Another study showed bacterial and physiochemical contamination of the waters of the Al-Kabir Al-Shamali River in the Al-Jindiriya area [19]. The importance of this research lies in evaluating the quality of water in the wells located in the vicinity of Wadi Al-Hada Center, in addition to the clear environmental effects of waste leaching on some groundwater wells located in the vicinity of it, especially after the appearance of turbidity in two wells located in Beit Ismael and Minya Yahmour villages. The research aims to monitoring and evaluating the quality of groundwater within ten wells located in five villages adjacent to the center of Wadi Al-Hada by determining some physical and chemical characteristics of groundwater in two wells from each village for a period of four months (until the results of the analysis became identical to the Syrian standard specifications) and determining measures to reduce the impact of major water pollutants.
MATERIALS AND METHODS
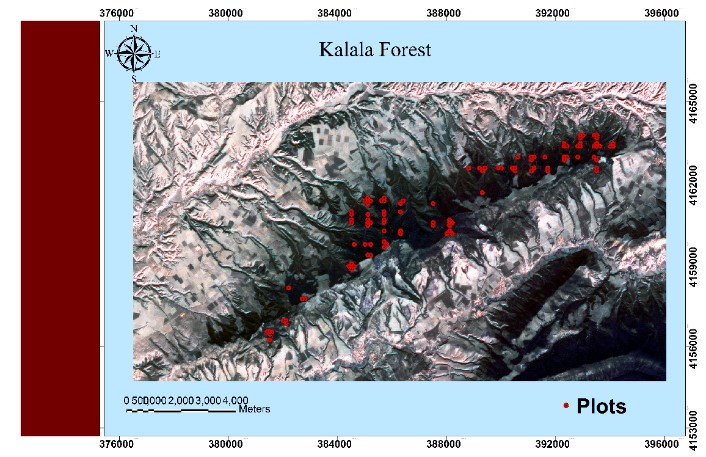
Study site and sampling sites:
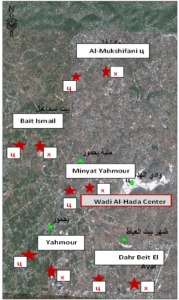
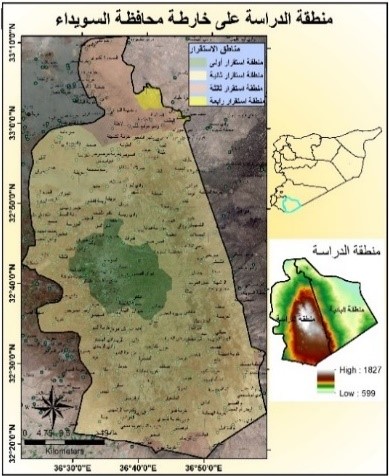
This research was conducted in the area surrounding the Wadi Al-Hada Center for Solid Waste Treatment, located in the village of Al-Fatasiyah, 13 km southeast of Tartous, and at an altitude of about 180 meters above sea level. The area of the center’s land is 100 dunums. several sites next to the center are used for dumping waste resulting from the center. The center is surrounded by a group of small villages and residential communities working in agriculture (these are the villages of Yahmour, Al Zarqat, Minyat Yammour, Karm Bayram, Beit Ismail, and others…) The irrigation of crops in these villages depends on groundwater. The idea of this research came from the appearance of detectable pollution in two wells located in Minyet Yahmour and Beit Ismail, due to exposure to waste leaching. The research was divided into two stages In the first stage, a survey was conducted by distributing questionnaires to local population. This questionnaire covered 50 families, and included questions to explore their opinions about the center, their health conditions, diseases suffered by family members, and the repercussions of water pollution on them due to the old dump and treatment center in Wadi al-Hada, and the availability of a sewage network in the area. In the second stage, the impact of Wadi Al-Hada center on some wells in five villages adjacent to it was studied as shown in Figure 1. Groundwater samples were taken from 10 artesian wells (Table 1) distributed in the region, so that they represent the various conditions of the site in terms of human activity and land use, and analyzes were conducted.
 Several field visits were made to the study site, and water samples were taken from these wells six times, at an interval of ten to twenty days. The sampling was stopped when the results became in conformity with the Syrian standard specifications starting from 7/27/2021 until 10/12/2021. Sample collection and analysis: Samples were collected in 1-liter polyethylene containers to determine the COD index and measure some electrolytes. The containers were washed well with distilled water and study site water three times before being filled; other samples were collected in 500 ml glass containers to determine the number of faecal bacillus FC. The containers were sterilized in an oven at a temperature of 250ºC for two hours Water analyses were conducted in the laboratories of the Directorate of Water Resources in Tartous Governorate, as follow:
Several field visits were made to the study site, and water samples were taken from these wells six times, at an interval of ten to twenty days. The sampling was stopped when the results became in conformity with the Syrian standard specifications starting from 7/27/2021 until 10/12/2021. Sample collection and analysis: Samples were collected in 1-liter polyethylene containers to determine the COD index and measure some electrolytes. The containers were washed well with distilled water and study site water three times before being filled; other samples were collected in 500 ml glass containers to determine the number of faecal bacillus FC. The containers were sterilized in an oven at a temperature of 250ºC for two hours Water analyses were conducted in the laboratories of the Directorate of Water Resources in Tartous Governorate, as follow:
Working methods:
Physical, chemical and bacteriological analysis were carried out in the laboratories of the Directorate of Water Resources in Tartous, according to the following: Some physical indicators (pH, turbidity, and electrical conductivity) were measured at the study site using newly calibrated field devices as follows:
FC – (fecal coliform count): FC was determined using the filtration method on 0.45-micron bacterial membranes and incubated with MFC agar culture medium at 37.5°C for 24 hours using the following equipment: Bacterial isolation chamber from Lab Tech, buchner funnel for filtering bacterial samples, a bacterial incubator from Memmert, a sterilization oven from Memmert, and an autoclave from SELECTA, model AUTESTER ST
RESULTS
At the beginning of the research, the wells in Minyat Yahmour and Beit Ismael were polluted, due to the exposure of the aquifer to pollution by the waste leaching collected next to the center, but when the leachate was collected, the results returned to the permissible limits according to the Syrian standard specifications shown in “Table2”.
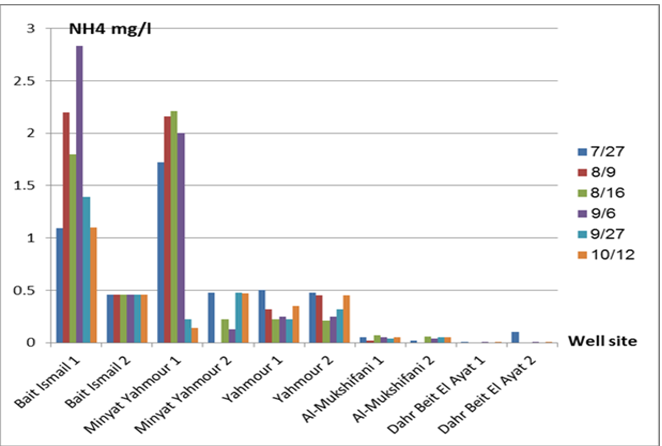
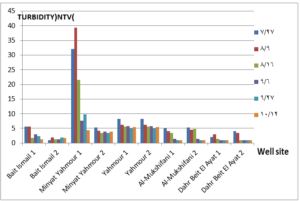
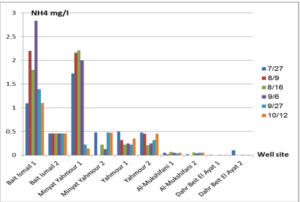
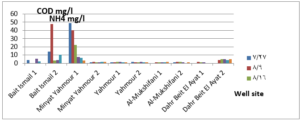
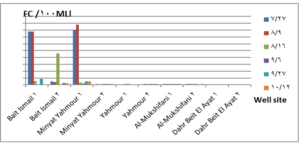
The pH values were moderate values tending to alkalinity, and were within the permissible limits according to the Syrian standard specifications and so was the electrical conductivity (Cond) which did not exceed 813 μM/cm in the wells. Whereas turbidity values were high in most of the wells in the first samples during July and August, especially in (well 2) Minyat Yahmour, where it reached (39ntu, 32ntu), and in (well 1) Yahmour (8ntu.2ntu) “Fig 2”. We also noted that the percentage of ammonia was above the permissible limits according to the Syrian standard specifications. “Fig 3”. COD values in all measurement locations exceeded the permissible limits according to the Syrian standard specifications (which is 2 mg/L) in the first samples, ( in July and August), “Fig 4”, and also the results of the bacteriological analysis showed high general count and a high number of coliform bacilli in the two wells located in Beit Ismail and well 2 located in Minyet Yahmour, “Fig 5” Finally, positive and negative electrolytes, It was noted that the values of the ions NO2-، NO3- ، PO43-، Cl-، SO42-did not exceed the permissible limits according to the Syrian standard specifications in the ten wells. Population survey results: The results of the questionnaire showed the occurrence of disease cases as a result of the use of contaminated well water.
DISCUSSION
We will graphically review only the indicators that do not conform to the Syrian standard specifications and analyze their changes spatially and temporally. The pH values were within the permissible limits according to the Syrian standard specifications. There was no significant change in them according to the change in the sampling date or the location of the well. As for turbidity, we noticed high turbidity values in most of the wells in the first samples, and we can attribute this to the leaching of pollutants from the landfill into the effluent that heads from Wadi al-Hada center towards Minyat Yahmour and Beit Ismail. Then, the values of turbidity decreased until it became within the permissible limits according to the Syrian standard specifications in November. This is because the problem was solved in the area and the leachate was collected in the rainwater collection basin and This is consistent with studies confirming the impact of landfill leachate on groundwater [20, 21] The measurements also indicated that the electrical conductivity values of well water and surface water were within the permissible limits according to the Syrian standard specifications (1500 µm/cm), but the ammonium ions in the water influenced by human activity as the nitrogen was presented in polluted water (urine and uric acid). The production of ammonium ion during the ammonification process indicates the recent existence of contamination with organic matter and the progress of the self-purification process that carried out by microorganisms in aquatic media. [22].COD values: It is noted from “Fig 4” that the COD index has increased, as the highest value was recorded in well 2 located in Minyet Yahmour and the two wells located in Beit Ismail, but these values began to decline until they became within the permissible limits in the month of November, and this indicated that the aquifer was contaminated with highly concentrated organic matter that may be due to the leachate from Wadi Al-Hada. The discrepancy in the results between the wells can be explained by the difference in the slope and permeability of the soil and rocks at this location compared to the locations of other wells [4] “Fig 5” shows the bacteriological analysis that it exceeded the permissible limit (which is zero) in all wells except for the (two wells) in Dahr Beit Al-Ayat and (well 1) in Minyet Yahmour,the value (zero) was recorded which was good . The largest value was in the two wells (well l) in Beit Ismail and ( well 2) in Minyet Yahmour, during the first three months (July, August and September). This may be due to the fact that there is sewage near them. As for the rest of the wells, the number of coliform bacilli was greater than zero, but it was relatively less than these wells and this is consistent with studies confirming the impact of waste leaching on the groundwater [23, 24] Positive and negative electrolytes: It was noted that the values of the ions NO2-, NO3-, PO43-, Cl-, SO42- did not exceed the permissible limits according to the Syrian standard specifications in the ten wells during the four months. This can be explained by the fact that they were not subjected to excessive fertilization, and this was indicated by many studies [25,26,27]; However, the results showed an increase in the concentration of ammonia ions in the two wells located in Beit Ismail and Minyat Yahmur. It was also found that there is no clear relationship between the depth of the well and the values of the pollution indicators in it. This can be attributed to the fact that the studied wells were not fed by the same aquifer [28]. It is important here to point out a study on Modeling the movement and transport of pollutants in the groundwater using GMS program (a quantitative model using MODFLOW, and a qualitative model using MT3D), which was conducted at (Al-Bassa Dump) [29], and the results of the quantitative modeling of the water resources system in the Al-Bassa Dump area resulted in obtaining a map of Head Contours and flow Budgets, and the ability to display cross-sections at any point of the studied area. We also were able, through qualitative modeling, to simulate the transport of pollutants, and the leakage of leachate from Al-Bassa Dump, and predict its expected changes during different periods. Therefore, it is necessary to emphasize the importance of using modeling programs to predict the movement of pollutants in the Wadi Al-Hada center area. Population survey results: The results of the questionnaire showed the occurrence of disease cases as a result of the use of contaminated well water, the most important of which were acute intestinal diarrhea and gastrointestinal infections. 30% of the surveyed people indicated that they were exposed to diseases because of the landfill or as a result of their use of groundwater wells, and most of them stopped using this water for drinking and only used it to irrigate crops. The results also showed that 80% of the population are farmers and have lived in the area for more than 50 years, and 25% of them depend on technical drilling.
CONCLUSIONS AND RECOMMENDATIONS
We can conclude from this study the following main points:
RECOMMENDATIONS
To avoid the health and environmental harms of the waste and sewage water, we recommend the following:
Use a modeling program to predict pollutants by constructing a mathematical model using GMS program (a quantitative model using MODFLOW, and a qualitative model using MT3D).
INTRODUCTION
Substitutes to cement are a sustainable way to decrease the overuse of cementitious materials, and it is gradually becoming important to include them in the building sector [1]. Energy consumption is the major environmental concern associated with cement manufacture, including the direct use of fuel to extract and transport the raw materials as well as the high energy required for calcination, which is provided by burning of coal, coke, natural gas, diesel and fuel. Cement manufacture consumes about 1758 kWh per ton of cement. Mortar is one of the decorative building elements in addition to its role as a binder for the block and is widely used in the construction field. The mortar mixture consists of Portland cement, fine aggregate, and water. Many adjustments have been made to the mortar concerning its components [2]. The various construction processes are one of the main sources of high carbon emissions, as the cement industry is a significant component in increasing carbon emissions. Using other cementitious materials to produce cement-based materials is an important technique to decrease carbon emissions, where the cement industry generates nearly 8% of global CO2 [1]. Fly ash and Silica fume (pozzolanic materials) are widely used as cement alternatives to produce cement-based materials [1]. The consumption of local raw resources is one of the obstacles to cement manufacture [3] [4]. In addition, issues related to climate change have attracted significant attention. However, more recently, issues related to local health aspects have been mentioned. Therefore, designers of building material mixtures seek to introduce sustainable technologies to reduce environmental impact [5] [6]. Current technological advances aim to improve the construction process in terms of speed, performance and financial productivity. The use of gypsum mixes that do not require high levels of heat during the production process is common [7]. Gypsum is a construction material known for its good performance against variations in humidity and its rapid ability to change shape and harden. However, gypsum materials have some disadvantages for use in construction, such as: not being hard or brittle, poor waterproofing and decomposing quickly. For this reason, many researchers have conducted numerous tests to determine and improve the performance of these materials. Archaeologists dated the earliest uses of gypsum about 7000 BC [8]. Many researchers aimed to replace raw building materials with wastes and biomass (low energy consumption binders) to increase the environmental efficiency of construction. Gypsum is considered one of these low-cost materials, that seems to be a suitable option for new constructions, in addition to being widely used in many restoration and rehabilitation operations for old buildings. The advantage in which gypsum is distinguished from cement and lime is its production at about 120-180 °C, with a much lower burning temperature and energy, while cement needs about 1500°C and lime needs about 900°C. Thus, the associated low energy makes gypsum a sustainable solution [9]. Concerning energy saving in buildings in European countries, around 75% of buildings need incomplete or complete repair because they are not energy efficient. Enhancing the performance of wall cladding (interior and exterior) is an important energy-saving technology as part of the rehabilitation and maintenance of damaged and older buildings [10]. As for Syria, this percentage increases very significantly as a result of the war that the country was exposed to, according to the observations of the authors themselves, to more than 90%. By the way, statistical reports issued by the International Energy Agency indicate that worldwide energy depletion in the building sector will reach 30% in 2060 if the existing ratio of increasing growth remains as it is now [11]. Accomplishing high energy efficiency in structures is the most demanding concern of governments internationally, which would cause a decrease in energy depletion and environmental problems related to CO2 emissions [11]. Various research projects and investigations began years ago to find suitable alternatives to reduce the concentration of carbon dioxide in the atmosphere, in addition to reducing the cost of building materials [12][13][14]. Unpredicted environmental hazards of carbon emissions resulting from cement manufacturing required for all structures in addition to depletion of raw resources are the most persistent tasks of future engineering. However, achieving sustainability by introducing natural materials that are affordable for various construction process is one of the preferable solutions. Due to the lack of searches done on JB, and its wide spread in the Deir ezzor region, it was necessary to draw attention to that product and define its specification. The key objective of this investigation is to determine the engineering properties of JB-based mortar. JB is used as a partial replacement of cement with varying ratios of 0%, 10%, 25%, 50% and 75% of the total cement weight. Then, comparative results between the cement mortars and JB-based mortar will be presented.
MATERIALS AND METHODS
JB: The southern region of Deir ezzor is generally famous as the extraction deposits of the raw material for the production of JB. A large number of limestone mountains, the most important of which are the southern mountains near the Qabr al-Wali area, the Hawooz area, the Tharda Mountains, and the ancient al-Jura area. A single limestone mountain mass is called a Maqtaa, it is a huge rocky mass that has a vertical cliff surface called a Gall. The chemical composition of JB was measured to determine its components (CaO, SO3, and H2O). Table 1 represents these compositions.
The different compositions of compounds are due to the heating process, which leads to the release of water and thus the restructuring of other molecules. After the trailer carries the load of stones to Namura, which is the main factory of the white JB, the workers collect the stones brought from the nearby mountain. Then the second phase begins when the workers, who are spaced about 2 meters apart, break these stones into sizes smaller than egg size, and then carry them manually to the dome of Al-Namoura, where they are distributed over its surface after being sieved so that the stones smaller than 2 cm in diameter are eliminated. After paving the dome with small stones, the third phase begins including the burning process, which lasts for two days. The purpose of the burning process is to separate the desert dust and impurities from the stones in addition to modifying the structure of the stones so that they become fragile and completely free of moisture. After one cooling day, the burned stones are taken to a stone grinder to be smashed into powder. The JB is manufactured from CaSO4⋅2H2O (gypsum), which is obtained from the mineral rock. Upon heating at a temperature of around 160°C, the gypsum converts to CaSO4.0.5H2O (JB) [16].
Experimental program
This section compares the performance of the cement mortar (0% of JB) with the cement-JB mixture mortar with different ratios of JB. Different specimens of mortar were prepared using the materials indicated in Table 2. The weight, volume and bulk density of cement, sand and JB are determined.
The proportions of the mortar components were as follows:
Cement, water and JB were mixed in a mixer for one minute before sand was added. The total mixing time is about 3 minutes to get good adhesion between the cement, Al Juss, sand and water. The cement used is local ordinary Portland cement (grade: 32.5, specific gravity: 3.15, finesse: 3360 cm2/gr, chemical composition: shown in Table 3), and the water used is safe to drink. As for sand the Table, 4 represents some specifications of the crushed limestone sand used. To accomplish the comparison, five mortar mixtures were prepared that differ from each other in the percentage of cement and Al Juss, while the control sample was produced using pure cement as a binder and four samples that include JB with different proportions 10%, 25%, 50%, and 75% of total cement weight.
![]()
RESULTS
The properties of the modified cement mortar were evaluated using JB binder. The compressive and other properties revealed lower values compared to the cement mortar. The following is a presentation of the results conducted during the study.
The finesse of Cement (Blaine value) vs. JB replacement
The relationship between the fineness of cement and the JB mixture with the used JB replacement ratios is shown in Figure 1.
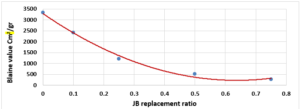
The fineness of the mixture decreases as the JB replacement ratios increase as shown in (Figure 1). The mixture’s fineness affects the workability, durability, strength, and hydration rate. This decrease is due to the increase in JB related to cement because it is finer than JB which was produced manually.
properties of fresh paste and mortar:
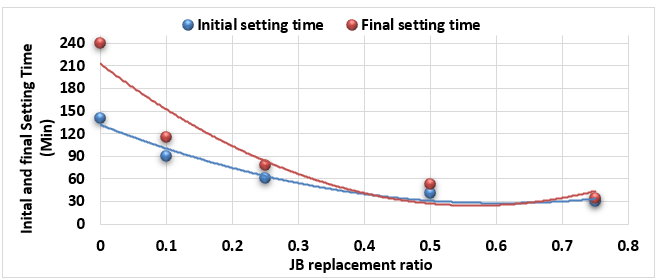
Study of Initial and Final Setting Times of Cement-JB vs. JB Replacement:
Figure 2 illustrates the relationship between the initial setting time and final setting time (measured according to ASTM C-191) of the mixture of cement-JB pastes with the JB replacement ratios.
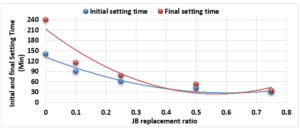
In the analysis of Figure 2, it can be noted how the initial and final setting times of the cement-JB mixture pastes decreased by increasing JB replacement ratios. At the 50% and 75% JB of the mixture, the initial and final setting times are close to each other. The decrease in both initial and final setting times of mixtures is due to the increase in JB, which causes them to lose their elasticity and become sufficiently rigid.
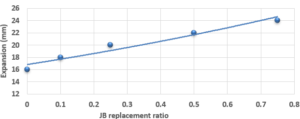
Study of Expansion of Cement-JB vs. JB Replacement according to Le Chatelier:
The expansion value of the cement and JB pastes versus JB replacement according to Le Chatelier is shown in Figure 3. The expansion value of the cement-JB mixture mortars increased by the increasing of JB ratios as shown in Figure 3. All of JB ratios do not show any significant expansion values. This increase is due to the fact that JB has a larger percentage of pore voids and is less homogeneous than cement, which was produced manually, and therefore has greater expansion values.
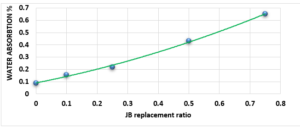
Study of Water Absorption value:
Figure 4 characterizes the water absorption value of cement-JB mixture mortars versus JB replacement, as the increase in the percentage of JB increases the water absorption value. JB is hydrophobic, as the increase in the percentage of JB increases water absorption value (In this case, I think that JB should be hydrophilic rather than hydrophobic). It can be clearly distinguished that all these values are less than 70%. Water absorption is the movement of liquid within unsaturated JB-cement samples’ pores under no external stress. JB, which possesses higher porosity, is known to have a more water absorption capacity, causing an increase in the absorption rate as JB content increases.
Properties of hardened mortar:
Compressive and Flexural Cement-JB Mortar Strength: Compressive and Flexural strength of the cement-JB mortar mixtures were determined at 2, 7, and 28 days of standard curing conditions (20 ± 2°C, and relative humidity >95 or immersed in water) as it is shown in Figures 5 and 6.
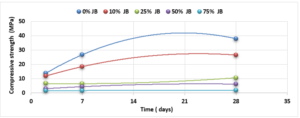
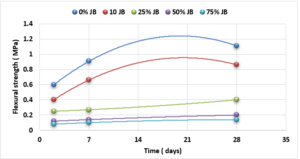
The values of compressive strength cement-JB mixture mortars are shown in Figure 5. The highest compressive strength can be clearly observed in the control samples (38 MPa), followed directly by mixtures containing 10% of JB (26.5 MPa), and then by 25% of JB (10.5 MPa). On the other hand, the lowest compressive strength of cement-JB mixture mortars was obtained at 75% of JB, reaching 1.9 MPa. Adding JB to cement causes an increase in the volume of the mortar, which leads to cracking of the bonds that connect the aggregates, thus reducing the compressive strength. The outcomes derived from the flexural strength tests are shown in Figure 6. This figure displays how the cement mixtures containing 10% of JB have higher flexural strength values than the other three JB ratios investigated (0.86 MPa). When JBs are added to cement, mortar volume expands, breaking bonds and reducing flexural strength.
Study the change of dry density according to the JB replacement ratios: The dry density of the cement-JB mixture mortars with the JB replacement ratios at 28 of curing days are shown in Figure 7.
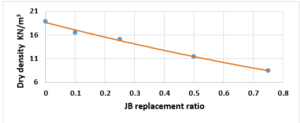
It can be simply detected that increasing the JB ratio decreases the dry density. Reducing density is attributed to certain physical properties, specifically the difference in specific gravity between JB and cement. Additionally, JB exhibits a higher porosity compared to cement, leading to increased volume and reduced overall density.
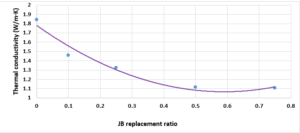
Investigation of the thermal conductivity (K-value) of the replacement of JB:To illustrate the relationship between thethermal conductivity of cement-JB mixture mortars versus JB replacement ratios, the K-value were determined. JB is categorized by low thermal conductivity against the cement mortar as shown in Figure 8, where the thermal conductivity decreases as the JB ratio increases. In general, as the JB content increased, the k-value decreased, because of its heat-insulating properties, as explained previously. The low K-value indicates that JB can be used as a suitable mortar for high-temperature applications.
DISCUSSION
Compared with the ASTM C1329 specification, the mortar cement-JB of 10% of JB can be used instead of type M mortar cement (20 MPa) [17]. While the mortar cement-JB of 25% of JB can be used instead of type S mortar (14.5 MPa), which is used in building parts for exterior, at or below grade, and that of 50% of JB may be used instead of type N mortar (6.2 MPa), which is used in building parts for interior non-load-bearing[17]. According to the ASTM specification, the cement-JB mortar of 10% of JB can only be used as type M mortar (0.8 MPa) [17]. While cement-JB mortars with other ratios of JB cannot be used. The initial setting time at 10% of JB is 90 min, which is in accordance with types S and M (not less than 90 min) According to the ASTM C403 specification. As for the final setting time, not more than 1440 min, all of the final setting times are smaller than this value. These setting times are important factors that affect the strength, durability, and workability of cement. For this reason, 10% of JB can be considered a suitable additive for cement within the standard limit to accomplish the best outcomes in building projects. The maximum expansion ratio at 75% reached 24 mm compared to 0% of JB, which was 16 mm. As for mortar with 10% of JB was 18 mm (only 2 mm increasing related to 0%). Thisconfirms that the JB does not display any considerable consequent expansion. If the expansion value is more than 10 mm, the JB-cement mortar is unreliable as described in ASTM specifications [17]. Consequently, the addition of JB had a positive outcome in the avoidance of the shrinkage property of cement that may lead to the formation of plaster cracks or deficiencies. A higher cement fineness provides very good quality, where smaller particles react faster than bigger particles. A cement particle that has a size of 10µm needs around 30 days to achieve the entire reaction, whereas a particle with a size of 1µm does not need more than 24 hours to achieve the entire reaction [18]. All of the water absorption ratios are less than 70%, which satisfies the conditions of ASTM specifications [17]. Cement mortar needs more amount of water (before and after applying, which causes the site to get very dirty) than the JB containing mortars, which means more time during the curing period in contrast with JB mortars that dry quickly and do not require any more treatment water. Mixing JB with cement at different proportions of 10%, 25%, 50%, and 75% of the cement weight does not considerably modify the dry density of the control cement mortar, which was about 18.9 KN/m3 and for the cement-JB mortar of 10%, 25% of JB was 16.5 and 15.1 KN/m3 respectively, and the reduction ratio relative to the control cement mortar was 14.5 %, 20% respectively. The two preceding types of cement-JB mortars are considered to be heavy-weight (greater than 15 KN/m3) [19]. Consequently, the addition of JB had a positive outcome in the avoidance of substantial volume changes, which lead to cracks in the plaster, or adherence deficiency to the wall support. The quantity of energy needed to cool and heat a building is reliant on the k-value [20]. The materials with a lower value of thermal conductivity have greater capability to restrain heat transmission. There are many factors affecting k-value such as mixture kind, percentage of fine aggregate, total volume of aggregate percentage, ratio of (W/C), humidity and temperature conditions, and additive types (fly ash silica fume, blast furnace slag) [20]. The results show that the thermal conductivity of cement-JB mortars increases as the ratio of JB of it gets larger. Thus such mortars are suitable for high-temperature applications and that is why the ancient residents of Deir EZZOR, whose weather is considered to be very hot, have been using the mortar of pure JB to cover their homes.
CONCLUSIONS
This paper presents the potential of combining JB and cement in the process of production of cement-JB mortars that may be used in the construction sector. Although the obtained compressive and flexural strength values were lower than those of control cement mortar, there is an encouraging outcome of the usage of JB in cement-JB mixture mortars, as the compressive strength at 10% of JB, meets the standard specification for type M cement mortar. Whereas the cement-JB mortar at 25% of JB may be used instead of type S mortar. The addition of JB to the cement mortars decreases the thermal conductivity, which gives good thermal properties and ensures energy saving. Cement mortar is prone to cracking, most cracks are caused by shrinkage, which is very common, while JB-added mortar has high elasticity and is less prone to cracking, All of the JB ratios do not show any significant expansion values, where the maximum ratio of 8 mm compared to 0% of JB. In addition, the JB is hydrophobic which results in the moisture not remaining on the interior walls for a long time which will cause no formation of mould and mildew on these walls and prevent them of being slippery. JB-cement mortar dries quickly, which has a 90 min initial setting time at 10% of JB, so it does not require any additional treatment water as the cement mortar which needs a great amount of it (before and after applying). The study also stated that increasing the JB ratio decreases the dry density; the reduction ratio was 14.5 %, 20% at 10%, 25% of JB, respectively. More particularly, it has been probable to confirm that the cement-JB mixture mortars with 10% or 25% of JB accomplish worthy properties, although these mortars do not meet the standards achieved by control cement mortars. On the other hand, the cement-JB mixture mortars may be used in rehabilitation works and rural buildings as a sustainable solution. Also, they can be used, as they were locally used, as interior coverage of walls and roofs in high-temperature cities like Deir EZZOR to reduce their thermal conductivity and make houses more thermally comfortable.

INTRODUCTION
Although coins and banknotes are in issues for decades, there is no agreement amongst economists on what is the theoretically optimal denomination structure of a currency [1]. Two components are usually used to identify any denomination structure, those being the structure boundary and the series within the boundary. The structure boundary includes determining the lowest coin value, the highest banknote value and the transition between coins and banknotes. The series inside the boundary includes the number of coins, banknotes, and total number of denominations [2]. Determining the optimal denomination structure of a currency is a daunting task. It involves ensuring the efficiency of the structure, its cost effectiveness and its balance in terms of having a proper mix of the various denominations [3] [4]. To ensure this task is well handled, central banks need to closely monitor the evolving changes (technology, security issues, high inflation..etc) and timely respond to them [5]. Empirically, [6] proposed the D-Metric model to determine the denomination structure of the currency. The model utilizes the relationship between the average daily wage level (D) and the denominations of the currency to identify the coins on the lower scale that need to be withdrawn from circulation, the boundary point between coins and banknotes, and the appropriate timing for the introduction of higher banknotes [7]. This study uses the D-Metric model to analyze changes in the denomination structure of the Syrian Pound between 1997 and 2022. The choice of the period is to capture the last three changes in terms of introducing a higher banknote in Syria. The study was motivated by the scarcity of previous research on the optimal denomination structure in general and in Syria, in particular. The study was further motivated by the public attention that accompanied the introduction of the SP5000 and the rumors regarding the potential issuance of the SP10000. The aim of this study is twofold. First, to analyze the denomination structure of the Syrian Pound and to verify whether the introduction of the last three high denomination banknotes was justified from the D-Metric model point of view. Second, to analyze whether a higher banknote should be introduced. The study contributes to the literature on the optimal denomination structure as it is the first that analyzes the denomination structure of the Syrian currency using the D-Metric model. The findings of the study have empirical implications for the Central Bank and the public in Syria. They will enable recommending the denomination of the higher banknote that should be issued and the timing of this issuance. The remainder of the study is organized as follows: Section one sheds light on the currency structure in Syria. Section two explains the D-Metric model. Section three analyzes the denomination structure in Syria using the D-Metric model. Section four concludes the paper.
The Currency Structure in Syria
The monetary authorities and denomination structure in Syria passed through several historical landmarks. Below is a brief highlight of this main historical changes. In the era of the French Mandate, the Bank of Syria supervised the process of issuing the currency. The name of the bank changed later on during that period to become the Bank of Syria and Lebanon. After gaining independence, the Bank of Syria and Lebanon continued on issuing the currency in both Syria and Lebanon. However, it was replaced later on by the Syrian Institute for Issuing Money. In 1953 the Legislative Decree No. /87/ was issued [8]. The Decree defined the basic monetary system in Syria and established a Council for Money and Credit to take on the tasks of the Central bank. The Central Bank of Syria did not officially start working until 1/8/1956. Below is a review of the development of the currency structure since the Central Bank of Syria became responsible for supervising the issuance of the Syrian Pound, the official currency in the Syrian Arab Republic. Figures (1) and (2) below show the development of the currency structure after the Central Bank of Syria became responsible for issuing the Pound. As per the structure of coins, after its establishment, the Central Bank of Syria continued to issue coins in the denominations of 2, 5, 25 and 50 Piasters and one Pound that previously existed. In 1960, a new coin in the denomination of 10 Piasters was issued for the first time. As shown in Figure (1), the structure of the coins remained unchanged until 1995, when new coins in the denomination of 25 Pounds were issued. In 1996, new coins in the denominations of 2, 5 and 10 Pounds were issued for the first time. In the same year, coins in the denominations of 2, 5 and 10 Piasters were withdrawn from circulation. In 2004, coins in the denominations of 25 and 50 Piasters were withdrawn from circulation. At the end of 2018, the highest denomination of coins, 50 Pounds, was issued [9]. With regard to the structure of banknotes, the Central Bank of Syria continued to issue banknotes in the denominations of 1, 5, 10, 25, 50 and 100 Pounds which previously existed. In 1958 a new banknote in the denomination of SP500 was issued for the first time. As Figure (2) reveals, the structure of banknotes remained unchanged until year 1997, when banknotes in the denominations of SP200 and SP1000 were issued for the first time. More than ten years in the Syrian crisis, which started in 2011, caused a massive economic destruction to the Syrian economy. The Syrian Pound which had a pre-crisis exchange rate on the average of USD1= SP45 gradually depreciated to exceed USD1= SP3800 in the black market. The depreciation of the Syrian Pound and the high inflation that Syria was facing triggered many questions regarding the necessity of issuing higher banknotes. In 2015, with the annual inflation rate reaching an average of 38.46%, the SP2000 note was printed for the first time. It was put into circulation in July 2017 when the annual inflation rate was 14.48% [10]. Recently, in 2021, a new note in the denomination of SP5000 was put into circulation. The 5000 note was printed in 2019 when the annual inflation rate was, on average, 13.42%] [10]. According to the official releases of the Central Bank of Syria, the SP5000 note was printed to meet the trading needs of the public in a manner that ensures facilitation of monetary transactions and reduces the cost and intensity of dealing in banknotes. The Central Bank reported that the current economic changes, and the significant rise in prices that started in the last quarter of 2019 and continued during 2020, made the timing appropriate for putting the SP5000 into circulation [10]. Following the issuance of the SP5000, there was a public debate on whether the SP10000 needs to be issued and put into circulation or whether it is premature to do so.
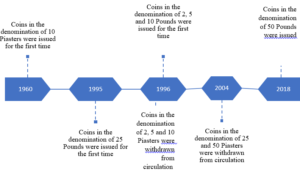 Figure (1): Timeline of the development of the coin structure in Syria
Figure (1): Timeline of the development of the coin structure in Syria
The following section introduces the D-Metric model that will be used to analyze the changes in the currency structure in Syria since the introduction of the three highest banknotes (SP1000, SP2000, and SP5000).
MATERIALS AND METHODS
The D-Metric model
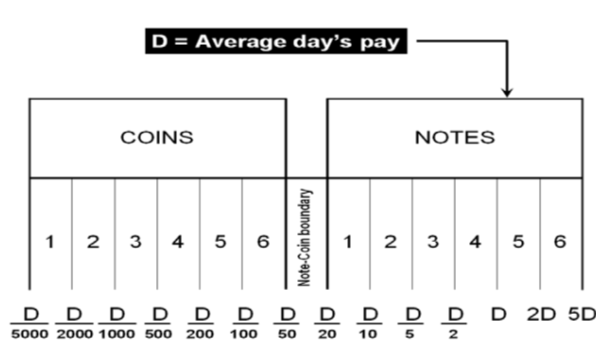
Determining the optimal denomination structure includes identifying the structure boundary and the series within the boundary. That is to say, identifying the lowest coin value, the highest banknote value and the transition between coins and banknotes along with the number of coins, banknotes, and total number of denominations inside the boundary. The spacing of the denominations in most countries is based on either a binary-decimal triplets system (1-2-5) or a fractional-decimal triplets system (1-2.5-5) [2]. Syria is amongst countries that adopted a mix of the two systems. It has six denominations of coins (1, 2, 5, 10, 25, and 50) and seven denominations of banknotes (50, 100, 200, 500, 1000, 2000, 5000). The denomination of (5, 10, and 25) banknotes are legal tender although they are not issued any more by the Central Bank. As can be seen, the denominations (10, 25 and 50) follow the (1-2.5-5) system while the rest of the denominations follow the (1-2-5) system. Trying to figure out the optimal denomination structure, [6] used data from sixty currency-issuing authorities around the world. They documented a consistent relationship between the average daily pay (D) in a country and its currency structure. They reported that in most of the examined countries, the boundary denomination between coins and banknotes is located between D/50 and D/20. The top and lowest denominations are around five folds of the average daily pay (5D) and 5000 parts of the average daily pay (D/5000), respectively [12]. As shown in Figure (3), the model assumes that there are six denominations of coins and six denominations of banknotes along with one denomination at the boundary between coins and banknotes. The model can be used to advise when a modification on the denomination structure is needed. This includes the modification of the lowest-highest denominations and the transition between coins and banknotes [2]. The D-Metric model, however, is subject to several limitations. First, it is a practical method that lacks a theoretical base. Second, it ignores other factors that should be taken into consideration when determining the denomination structure of a currency. This includes, the costs associated with economic agents and users’ preferences, including payment habits [13] [14] [15]. The model also ignores the fact that payment habits, culture and wealth holding might differ across countries and could vary, within the same country, over time. In addition, the model fails to take into account the durability of monetary items and their costs when determining the boundary point between coins and notes [2]. Despite being subject to several limitations, the simplicity of the D-Metric model makes it used as a guideline to the re-denomination of currencies and it has been successfully applied in a wide range of countries around the globe [12] [16] [17]. The following section will utilize the D-Metric model to analyze the denomination structure in Syria between 1997-2022.
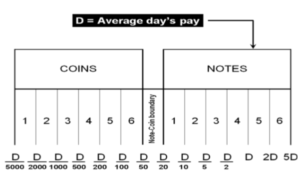
RESULTS
As Figure (2) indicated, bigger banknotes were issued in 1958, 1997, 2015 and 2019. Our analysis of the denomination structure in Syria is limited to years 1997, 2015 and 2019. Year 1997 was chosen as it experienced the last issuance of a higher banknote, the SP1000, prior to the eruption of the Syrian crisis.[1] Years 2015 and 2019 were chosen as they are the years in which the two higher banknotes, the SP2000 and SP5000, were issued. Years between 1997 and 2015 were not examined as there are no issuance of higher banknotes in these years. As highlighted earlier, the D-Metric model relates the average daily wage level to the denomination structure of the currency. Due to data availability issues, the nominal GDP per capita per day was used as a proxy for the average daily pay (D in the D-Metric diagram). The daily GDP per capita was adopted by many authors on their application of the D-Metric model [2] [12]. Table (1) reveals the value of D and the denomination structure in each of the examined years.
DISCUSSION
Starting with year 1997, the D-Metric model suggests that the lowest useful coin should be between SP0.02 (D/5000) and SP0.067 (D/2000). The note-coin boundary should be between SP2.7 (D/50) and SP6.7 (D/20), suggesting that the higher coin should be SP5, which can be either a coin or a banknote. The largest banknote suggested by the model is the SP500 banknote which falls between SP271 (2D) and SP677 (5D). Table (1), however, reveals mismatches between the theoretical denomination structure suggested by the D-Metric model and the actual structure in year 1997. To be more specific, the lowest coin, 25 Piasters (SP0.25), lies between D/1000 and D/500 instead of D/5000 and D/2000, as suggested by the model, and the highest coin is SP25 instead of SP5.[2] In addition, the SP10 and SP25 exist in coins and banknotes whereas the model predicts that the note-coin boundary should be SP5. Another mismatch with the D-Metric model is the existence of the SP1000 banknote whereas, according to the model, the highest banknote should be SP500 (between 271 and 677.9). Accordingly, based on the D-Metric analysis of the currency structure in year 1997, one can conclude that the structure is not the optimal one and that the introduction of the SP1000 was premature and should have been postponed until year 2005 when 5D was equal to SP1124.219. The structure recommended by the D-Metric model changes in 2015 in comparison to that in 1997. As shown in Table (1), the SP25 got pushed into the note-coin boundary whereas the SP5 and the SP10 fell into the coin category. Furthermore, the SP2000 banknote became the largest useful banknote. Unlike the mismatch in year 1997, it seems that the currency structure in 2015 complies with the theoretical denomination structure suggested by the D-Metric model in this year. The highest coin in circulation in 2015, SP25, falls into the note-coin boundary (D/20=619.989/20=30.999) and (D/50=619.989/50=12.399) and the highest banknote, SP2000, falls between (2D=2*619.989=1239.978) and (5D=5*619.989=3099.945). Therefore, it was appropriate, then, to issue the SP2000 banknote in this year. In fact, it was even appropriate to issue it in 2014, when D was SP471.6 (2D=943 and 5D=2358) [11]. Since the SP2000 was printed in 2015 but not put into circulation until 2017, the analysis requires examining whether it was put into circulation on the right timing. Knowing that in year 2017, D was equal to SP1053.99, the SP2000 falls outside what is suggested by the model (2D=2107.98 and 5D=5269.95). Accordingly, the delay in introducing the SP2000 into the market was inconsistent with the denomination structure suggested by the D-Metric model. In fact, the D-Metric analysis suggests that the SP5000 banknote could have been put into circulation in 2017 and not just the SP2000. As can be seen from Table (1) the structure recommended by the D-Metric model changes in 2019 in comparison to that in 2015. The SP50 got pushed into the note-coin boundary whereby the SP25 fell into the coin category. Furthermore, the SP5000 banknote became the largest useful banknote (lying between 2D=1437.641*2=2875.28 and 5D=1437.641*5=7188.2). The Table also reveals that the lowest useful coins for this year, SP1 and SP2, fall within D/2000-D/1000 and D/1000-D/500, respectively. The lowest useful banknote, SP50, falls into the note-coin boundary (between (D/50=1437.641/50=28.75) and (D/20=1437.641/20=71.88)). This means that the decision to issue the SP50 coin was appropriate. Adhering to the 1-2-5 system of spacing, the next useful banknotes would be 100, 200, 500, 1000, 2000, 5000 according to the model. Indeed, those are the currencies that are actually in circulation in that year. Although it is justified to put the SP5000 banknote in circulation since 2017 as indicated above, the note was not put in circulation until 2021.
Should a higher banknote be put into circulation?
Recently, there are discussions among the public and economists regarding the necessity of issuing a higher banknote (the SP10000 banknote). Issuing higher banknotes has its own advantages and disadvantages. One of the main advantages is the easy handling of transactions as people do not have to carry large quantities of money to do their daily transactions [20]. This is especially important bearing in mind the high reliance on cash and the very low reliance on E payment in Syria. Another advantage is the lower carrying and management expenses, as according to the Central Bank of Korea, issuing the higher denomination allowed a saving of 60 billion won (approximately USD 50,000,000) every year due to reductions in management expenses especially those related to logistic costs [21]. In addition, the higher notes have lower production costs as they are less frequently used and used with more caution than is the case for smaller notes [13]. The higher notes could also help reduce spending as people are less encouraged to buy something if they have to pay one big note than is the case if they are paying with several smaller notes [13]. Issuing higher notes might also protect the national identity of the country by reducing the chances of substituting the domestic currency for other currencies (dollarization) [22]. The major disadvantage of issuing higher banknotes, lies on the inflationary impact of issuing higher notes, which could be a very serious one. As expectations of inflation drive up inflation, the higher note might be followed by higher inflation. The fear is that if the cycle starts, it is not easy to stop it. More precisely, if inflation increases after the issuance of the higher banknote, this might lead to the issuance of a higher note and the cycle goes on. Other disadvantages of issuing a higher note revolves around production costs, susceptibility to forgery and facilitation of drag dealing and illegal activities [23] [24]. To determine whether a higher note, the SP10000, should be issued, we applied the D-Metric model on the daily GDP per capita for the year 2020 where D is equal to SP2101.06 [11]. As highlighted earlier, according to the model the highest note should be between 2D and 5D. This means that the highest note should be between SP 4202.12 and SP10505.3. Accordingly, the D-Metric model suggests that the SP10000 could have been issued and put into circulation since 2020. The high inflation that Syria is still facing makes us in doubts of whether a higher banknote should be issued as the SP10000 might not be enough to meet the needs of the daily transactions. Table (2) reveals the results of applying the D-Metric model on the daily GDP per capita for the year 2021 where D is equal to SP3099.93 [11]. As the table reveals the 2D and 5D are 6199.86 and 15499.65 respectively. This indicates that the 10000 note is enough and no higher note needed to be issued in that year. Unfortunately, no data of the daily GDP per capita for the year 2022 is available to conduct the analysis. To circumvent this issue, we tried to extrapolate the expected growth rate based on the historical growth rate, under two scenarios. In the first scenario, we used the daily GDP per capita in years 2015 and 2021 to calculate the average growth rate for the period.[1] This was then used to project the future daily GDP per capita on the following years. In the second scenario, we assumed that the growth rate on the daily GDP per capita between years 2020 and 2021 would remain unchanged, and we used this growth rate to project the future daily GDP per capita on the following years. Table (2) reveals the results of applying the D-Metric model based on both of the simulated scenarios. As Table (2) reveals, applying the average growth rate for the period 2015-2021 shows that the issuance of the SP20000 could be done in 2023 and should not be pushed beyond 2024. However, applying the aggressive growth rate, the one that is based on the growth rate of years 2020-2021, reveals that the issuance of the SP20000 could be done in 2022 and should not be pushed beyond 2023. The fact that the SP10000 could have been issued and put into circulation since year 2020 and that the SP20000 should not be pushed beyond 2023-2024, indicates that the monetary authorities might have to issue both of the banknotes, 10000 and 20000, at one time or within a short time span. This, however, might have adverse outcomes on the inflation levels that are already high!
CONCLUSION AND RECOMMENDATIONS:
The aim of this study was to analyze the denomination structure of the Syrian Pound between 1997 and 2022 and to examine whether the decisions of issuing the higher banknotes (SP1000, SP2000 and SP5000) were justified based on the D-Metric model predictions. The study also aimed to examine whether higher banknotes (SP10000 and SP 20000) need to be issued and put in circulation and what is the appropriate timing for this. The study was mainly motivated by the recent issuance of higher banknotes in Syria along with expectations of further issuance of higher banknotes. When comparing the denomination structure in the examined period with that suggested by the D-Metric model, the findings revealed that the introduction of the higher note, SP1000, in 1997 was premature and should have been postponed to 2005, however the issuance of the SP2000 was on the right timing. The delay however in putting the SP2000 in circulation was not consistent with the outcomes of the D-Metric model. The SP2000 was put into circulation in 2017 when it was appropriate to issue the SP5000. The findings also reveal that the issuance of the SP5000 in 2019 was consistent with the predictions of the D-Metric model. When examining whether a higher banknote, SP10000, should be issued, the D-Metric model suggests that the SP10000 could have been issued and put into circulation since 2020. The high inflation that Syria is facing now tempted us to examine whether the SP20000 should be issued. To overcome the lack of data on daily GDP per capita after 2021, we used two growth scenarios to simulate the daily GDP per capita for the coming years. The findings indicate that the SP20,000 should not be pushed beyond 2023-2024 the latest. The fact that the issuance of the SP20000 should not be pushed beyond 2023-2024 and that the SP10000 could have been issued and put into circulation since 2020 means that the monetary authorities should not delay the issuance of the SP10000 anymore. Otherwise, the monetary authorities might have to issue the two notes SP10000 and SP20000 at the same timing or within a very short time span. This, however, might have detrimental impact on the public confidence in the currency and might trigger higher and higher levels of inflation. Although the analysis was based on the simple and easy to apply D-Metric model, the popularity of the model among central banks and the cross-country empirical evidence that supported its predictions, allow us to utilize it. The findings obtained when applying the model have important implications to the monetary authorities in Syria. They, the findings, indicate that delaying the issuance of a higher note creates further problems in terms of having to issue a further higher banknote soon, which increases the uncertainty in the market and could create higher inflationary expectations. The findings are also of high importance to the public as finding the optimal currency structure enhances the efficiency of cash payment’s settlement. Despite the important findings of the current study, they should be interpreted with caution due to several reasons. First, as highlighted earlier, the D-metric model relates the average daily pay in an economy and the currency denomination structure, however, it does not take into account other factors that affect the denomination structure. This includes amongst other things, the cost structure and economies of scale associated with the printing and minting of a currency, the presence of extra demand on specific denominations, laws and regulations, public’s perception of inflation, etc. The currency denomination structure of a country is also a function of its past economic and political events which is not taken into account by the D-Metric model [12]. Two areas for future research emerge from this study. First, a multidimensional study that takes into account other factors that could affect the denomination structure is needed to get a better understanding of the suitability of the current and future denomination structures. Second, as issuing higher notes could be a response to the higher levels of inflation, the bidirectional relationship between issuing higher notes and inflation would be very informative to the monetary authorities and the public as very little evidence exists on this area.
Journal:![]() Syrian Journal for Science and Innovation
Syrian Journal for Science and Innovation
Abbreviation: SJSI
Publisher: Higher Commission for Scientific Research
Address of Publisher: Syria – Damascus – Seven Square
ISSN – Online: 2959-8591
Publishing Frequency: Quartal
Launched Year: 2023
This journal is licensed under a: Creative Commons Attribution 4.0 International License.