Prognostic Significance of Lactate Dehydrogenase (LDH) in COVID-19 Morbidity and Mortality



No doubt we live in a world dominated by technology; communication turned easier, accessible knowledge at our fingertips, AI performs everyday tasks, improved healthcare, work became available from home or everywhere in many cases, easy shopping, etc.
However, with this bloomed picture, comes serious threats of technology domination and control of our lives. In fact, generative AI per se threatens tens of careers and professions, not to mention the danger of becoming out of control in certain domains. The “bad” face of technology appears in many military applications that use high tech in destruction and killing. Likewise, technology burst has an eminent social impact, where poor countries become poorer while rich countries become richer, expanding the already vast gap between the two.
For Syria, striving hard to come out more than a decade of military and economical war, technology transfer suffered from many hurdles, including tech embargo and dwindling national economy. Nevertheless, the number of experts in many technology domains decreased. Hence, it is a crucial mandate for Syrian officials to put exceptional efforts to compensate for that loss. Boosting R&D activities at Syrian universities and research centers is the first and most important step, since relevant indicators clearly show a straightforward correlation between R&D activities and the ability for adapting frontier technologies.
The Syrian Journal for Science and Innovation (SJSI) was a humble attempt to shed light on Syrian innovative research in various sectors. After one and a half years since SJSI commencement, the journal succeeded in attracting solid Syrian researchers and was able to publish six consecutive issues in addition to one special issue, despite all unenthusiastic environment, nationally and regionally. In reality, we are very proud of the continuity of this journal and the knowledge accumulated since the first issue, hoping SJSI continues to nourish in the coming years as a valued tool for disseminating knowledge created at Syrian academic and research centers.
INTRODUCTION
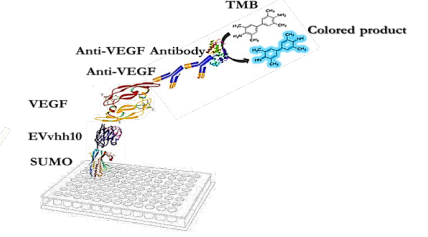
Angiogenesis, the branching out of new blood vessels from pre-existing vasculature, occurs physiologically during embryogenesis, the female reproductive cycle, and wound healing (1). It is also a crucial process in a variety of pathological conditions, including tumor growth, metastasis (2, 3), ischemic diseases, diabetic retinopathy (4, 5), chronic inflammatory reactions, age-related macular degeneration, rheumatoid arthritis, and psoriasis (6). Vascular endothelial growth factor (VEGF) is the most potent and predominant regulator of angiogenesis described to date (7, 8). This angiogenesis factor can instigate numerous biological responses in endothelial cells (ECs), such as survival, proliferation, migration, and vascular permeability, as well as the production of proteases and their receptors, creating prime conditions for angiogenesis (9, 10). It is estimated that up to 60% of human cancer cells express VEGF to create the vascular network necessary to support tumor growth and metastasis. Inhibiting angiogenesis has become an intensely investigated pharmaceutical area and represents a promising strategy for the treatment of cancer and several other diseases (11). Because of its central role in pathological angiogenesis, VEGF is a major therapeutic target. Strategies aiming to block the binding of VEGF to its receptors or to block intracellular signaling events form the basis of many new developments in anti-angiogenic cancer therapy (12). Numerous substances have been developed as angiogenesis inhibitors, some of which have already been approved for clinical use. These include monoclonal anti-VEGF antibodies (bevacizumab and ranibizumab) (13), anti-VEGF aptamers (pegaptanib), and VEGF receptor (VEGFR) tyrosine kinase inhibitors (sorafenib and sunitinib) (14, 15). Single-domain antibodies, also known as nanobodies or VHHs, possess valuable characteristics such as effective tissue penetration, high stability, ease of humanization, efficient expression in prokaryotic hosts, and high specificity and affinity for their respective antigens. Consequently, they can be introduced as alternative therapeutic candidates to traditional antibodies. VHHs represent the smallest functional unit of an antibody, preserving all of its functions, and due to their minimal size, they are also recognized as nanobodies (16, 17). Studies conducted by Shahngahian and colleagues in 2015 demonstrated that VEvhh10 (accession code LC010469) has a potent inhibitory effect on the binding of VEGF to its receptor (18). This VHH exerts its inhibitory role by binding to the VEGF receptor binding site. Among the members of the VHH phage display library, VEvhh10 possesses the highest binding energy at the VEGF receptor binding site, covering vital amino acids involved in the biological activity of VEGF and disrupting its function (18). The conventional expression of nanobodies in E.coli faces several challenges, primarily stemming from their small size and complex folding requirements. Nanobodies often exhibit low solubility, leading to the formation of inclusion bodies and hampering their functional utility. Moreover, the intricate disulfide bond formation and protein folding pathways of nanobodies make them prone to misfolding and aggregation within the bacterial cytoplasm (19-21). One standard method for expressing non-fused VHH is the use of E. coli expression systems. However, expressing non-fused VHH using conventional cytoplasmic expression methods in this prokaryotic system often faces challenges, including low expression, poor solubility, and misfolding of the antibody in E. coli (22-24). To overcome these shortcomings, we chose a novel expression system using a small ubiquitin-related modifier (SUMO) molecular partner (25, 26). SUMO Fusion Technology has emerged as a powerful tool for enhancing the soluble expression of proteins, including nanobodies, in E. coli. By fusing the target protein with the SUMO protein, researchers can promote proper folding, enhance solubility, and increase expression yields. SUMO fusion tags facilitate protein purification and can be cleaved post-purification to yield the desired protein product in its native form (27). SUMO is covalently attached to other proteins and plays roles in post-translational modifications (28). These roles include significantly increasing the yield of recombinant proteins, facilitating the correct folding of the target protein, and promoting protein solubility (29). The aim of this study was to develop an alternative method for more efficient production of VHH nanobodies in an E. coli-based expression system using the SUMO fusion tag. The SUMO fusion tag improves the solubility and yield of VHHs. Our results demonstrated that SUMO is very effective in promoting the soluble expression of VHH in E. coli. The resulting recombinant bioactive VHH can be used for therapeutic applications and clinical diagnosis in the future.
MATERIALS AND METHODS
Molecular and Chemical Materials
The materials, chemicals, and reagents required for the lab are listed as follows:
Ampicillin, kanamycin, and agarose from Acros (Taiwan), IPTG from SinaClon (Iran)
Ni-NTA resin from Qiagen (Netherlands), Plasmid extraction kit and gel extraction kit from GeneAll (South Korea), Enzyme purification kit from Yektatajhiz (Iran), Restriction enzymes HindIII/XhoI, ligase enzyme, and other molecular enzymes from Fermentas (USA), Pfu polymerase and Taq polymerase from Vivantis (South Korea), Primers from Sinagen (Iran), Methylthiazole-tetrazolium (MTT) powder from Sigma (USA), Penicillin-Streptomycin, Trypsin-EDTA, and DMEM-low glucose from Bio-Idea (Iran), Fetal Bovine Serum (FBS) from GibcoBRL (USA), Monoclonal conjugated anti-human antibody with HRP from Pishgaman Teb (Iran), Anti-Austen antibody from Roche (Switzerland), Other chemicals from Merck (Germany). Schematic 1 shows a schematic diagram of the construction of the pET-28a-SUMO-TEV-VEvhh10 Gene using SnapGene v5.1.5.
First, suitable primers were designed by OligoAnalyzer to isolate the SUMO gene sequence (see Table 1). The plasmid was used as a template for the polymerase chain reaction (PCR). Amplification was performed using the Pfu polymerase enzyme in a thermal cycler, utilizing the software we designed for this research (see Table 2). Different temperatures were tested (58, 59.5, 61, 62.5, 64) for primer annealing to the PCR template, with 58 °C being selected as the optimum temperature. The restriction enzyme sites were incorporated at the beginning and end of the primers. Additionally, the TEV protease cleavage site was placed between the SUMO and VEvhh10 sequences.
Gene Cloning: Primers for the amplification of the VEvhh10 gene with the accession code LC010469 were initially designed (Table 3). The plasmid containing the gene fragment served as a template for the PCR reaction. Amplification was carried out using Taq polymerase and Pfu polymerase enzymes in a thermocycler with a programmed temperature profile (Table 4). Various annealing temperatures for primer binding to the template were tested, and a temperature of 65°C was found to be the optimal annealing temperature. Primer cutting sites at the beginning and end of the Gene were designed, and the location of the TEV protease enzyme cutting site was positioned between the SUMO and the VEvhh10 sequence.
The gene fragments of SUMO and VEvhh10, amplified using Pfu polymerase via PCR, were extracted from the gel. Simultaneously, the amplified fragments and the pET-28a vector were digested using the BamHI and XhoI restriction enzymes. Purification was carried out using a commercial enzyme purification by GeneAll kit. Subsequently, the gene fragments were ligated into the target vector using T4 DNA ligase enzyme. The resulting ligated product was incubated overnight at 4°C. The ligated product was then transformed into E. coli DH-5α bacteria. To confirm the insertion of the Gene into the vector, the transformed bacteria were plated on kanamycin antibiotic-containing LB agar plates. Finally, the obtained colonies underwent Colony PCR using specific primers targeting VHH, T7 promoter, and terminator regions. The PCR products were analyzed on a 1% agarose gel, and positive transformants were screened and cultured further. The non-recombinant plasmid was purified using a plasmid extraction kit, and enzymatic digestion was performed to confirm the insertion of the gene fragment into the plasmid.
Expression and Soluble Detection of Recombinant SUMO-VHH
As depicted in Schematic 2, the pET-28a plasmid containing SUMO and VHH was transformed into E.coli BL21 (DE3) expression host cells using the heat shock method. The accuracy of transduction was confirmed by isolating colonies grown on LB agar medium supplemented with 50 mg/mL kanamycin. To express the genotype protein, a colony of bacteria containing the recombinant expression plasmid was inoculated into 10 mL of LB culture medium supplemented with 50 mg/mL kanamycin antibiotic and incubated at 37°C with optimal aeration at 250 rpm. Subsequently, 1 mL of mature bacteria was transferred to 50 mL of LB medium containing kanamycin antibiotics and incubated at 37°C until the OD600 reached approximately 0.6. Expression was induced by adding 0.5 mM IPTG and continued for 22 hours at 25°C. Following expression, the resulting product was centrifuged at 4000 rpm for 15 minutes at 4°C, and the bacterial cells were sonicated in lysis buffer (pH 8). The sonication product was centrifuged again at 12,000 rpm for 20 minutes at 4°C, and the supernatant was analyzed using the SDS-PAGE method (30). Proteins were purified by gradient chromatography using a nickel agarose column. The protein sample was transferred to the column pre-equilibrated with wash buffer (50 mM Tris-base, pH 8.0, 300 mM NaCl, 20 mM imidazole). Proteins that did not bind to the column due to the lack of histidine sequence were removed. Only the target protein remained attached to the column due to the presence of the histidine sequence. The bound proteins were eluted using elution buffer (50 mM Tris-base, pH 8.0, 300 mM NaCl, 250 mM imidazole). Purification was conducted using cold buffers to prevent thermal degradation of the proteins. Protein concentration was determined using the Bradford method with BSA as the protein standard (31).
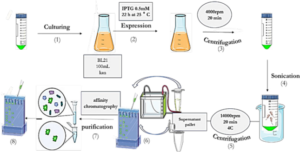
The expression and purification of VEGF8-109
The His-tagged VEGF8-109-RBD was expressed in E.coli BL21 (DE3) bacterial cells and subsequently purified using a Ni-NTA agarose column, following previously described protocols with slight modifications (32). Protein expression and purification were analyzed through sodium dodecyl sulfate-polyacrylamide gel electrophoresis (SDS-PAGE) and Coomassie Brilliant Blue R250 staining. To remove excess salt, the purified protein was dialyzed three times against phosphate-buffered saline (PBS) containing 10% (v/v) glycerol at 4 °C for 12 h. Protein concentration was estimated using the Bradford assay, with BSA as a standard (31).
ELISA-Based Immunoassay
The designed immunoassay is shown in Schematic 3. First, 100 μL of SUMO-VHH recombinant protein in carbonate-bicarbonate buffer was added to each well of a cell ELISA and incubated for 16 hours at room temperature. After 16 hours, the supernatant solution was dried and washed three times with 100 μL of PBS buffer. The blocking step was performed using a PBS solution containing 2% gelatin in a volume of 350 μL and placed at 37°C for 1 hour. Subsequently, the blocking buffer was dried and washed three times with 100 μL of PBST buffer (PBS + 0.05% Tween-20). Next, 100 μL of serially diluted VEGF solutions (ranging from 0.5 ng/mL to 1000 ng/mL) were added to the wells and incubated for 2 hours at room temperature. After incubation, all wells were dried and thoroughly washed three times with PBST buffer. Following this, 100 μL of human anti-VEGF monoclonal antibody at a concentration of 1000 ng/mL was added to the wells. After washing with PBST, 100 μL of HRP-conjugated anti-human IgG antibody was added to each well and incubated in the dark at 37°C for 1.5 hours. Subsequently, 100 μL of TMB was added to each well and incubated for 15 minutes in the dark. Finally, 100 μL of 2 N sulfuric acid was added to each well, and the absorbance of the wells was read at a wavelength of 450 nm (33).
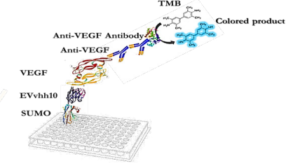
RESULTS
Products of the PCR Reaction
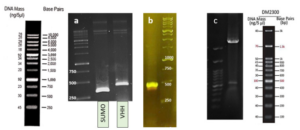
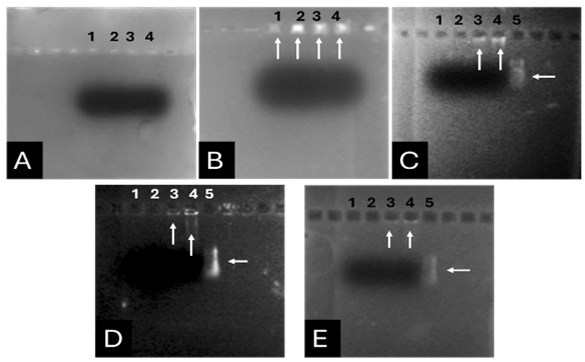
Based on our previous study (34), the VEvhh10 gene was amplified using pfu polymerase at an annealing temperature of 65 °C as showed in (Fig. 1).
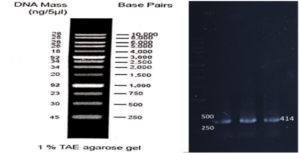
Construction of pET28a-SUMO-VHH Expression Plasmid
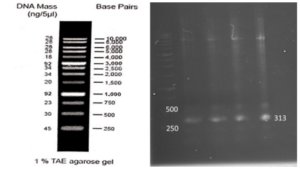
As depicted in (Fig. 3), the VEvhh10 product (402 bp) was amplified and double digested using HindIII and XhoI enzymes. The resulting product underwent purification in the preceding steps. The SUMO product, generated by the Pfu enzyme, was double digested using HindIII and BamHI enzymes, and the product (304 bp) was purified. Additionally, the plasmid pET28a was double digested using BamHI and XhoI enzymes, and the resulting product was also purified in preparation for the conjugation process.
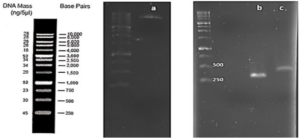
After joining the aforementioned sequences with the presence of the T4 DNA ligase enzyme, the respective products were incubated at 4°C for 14 hours and transformed into E. coli DH5α. The transformed product was cultured on a kanamycin plate, as shown in (Fig. 4.b). Agar plates containing the antibiotic ampicillin were labeled as a negative control, as depicted in (Fig. 4.a). Subsequently, in (Fig 4. c), some samples were isolated and confirmed using colony PCR by specific primers related to the T7 Promoter and Terminator, as shown in (Fig 4.d), and specific primers related to VHH, as depicted in (Fig. 4.e).
Confirmation of Gene Cloning
A fresh single colony was grown in LB agar containing the antibiotic kanamycin, and the extracted plasmid was used as a template to amplify the target gene and construct the SUMO-VHH. This step aimed to confirm the correctness of the gene cloning stage. PCR was carried out using the Forward and Reverse primers of the VEvhh10 gene (414 bp) and SUMO gene (approximately 310 bp), as depicted in (Fig. 5.a), as well as the Forward T7 promoter Reverse SUMO primers (approximately 470 bp), as shown in (Fig. 5.b). To ensure further reassurance, the plasmid was double digested using the cutting enzymes BamHI and XhoI. The double enzymatic digestion process was performed, and the desired Gene was observed on the gel, as illustrated in (Fig. 5.c). The results indicated the success and confirmation of gene cloning.
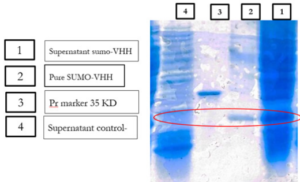
Expression and Purification of the SUMO_VHH
E.coli cells harboring SUMO-VHH were induced by 0.5 mM IPTG for 22 h at 25°C. The cell pellets were harvested by centrifugation, and protein was extracted and separated by sonication and centrifugation. The supernatants and precipitate were collected and subjected to 12% SDS-PAGE analysis. As depicted in (Fig. 6), the expression of a 24 kDa protein, similar to the predicted size, was induced by IPTG, compared with the negative control (blank plasmid) or recombinant bacteria without IPTG induction.

Previous studies have indicated that recombinant antibodies often form inclusion bodies using traditional E. coli expression methods (35). Our results suggest that SUMO is very helpful in promoting the soluble expression of VHH (36). To obtain high-purity recombinant protein, Ni-NTA chromatography was employed for purification because the 6His-tag was located in the N-terminal of SUMO. Different concentrations of imidazole were tested to elute the recombinant protein. The results showed that SUMO-VHH was efficiently eluted from the Ni-NTA column using an elution buffer containing 250 mM imidazole. SDS-PAGE analysis demonstrated that the purity of SUMO-VHH exceeded 90%, as shown in (Fig. 7).
Expression and Purification of Recombinant VEGF 8-109
As indicated by our previous research, recombinant VEGFRBD8-109 was produced in soluble form in E. coli BL21 (DE3) strain after induction for 22 hours at 24°C. Purification of the His-tagged fusion protein was performed using Ni-NTA affinity chromatography. The activity of the unconjugated VEGF RBD 8-109 produced was also evaluated through its effect on the growth and proliferation of human umbilical vein endothelial cells (HUVECs) using the MTT assay (37, 38). Cell proliferation was good with an increase in the concentration of unfused VEGF RBD 8-109. At a concentration of 240 ng/ml, the cell count reached approximately 80% compared to the sample lacking VEGF8-109 (34). Accordingly, it can be used in VHH-SUMO binding assays.
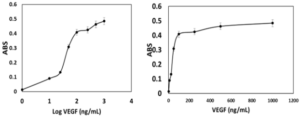
Investigating the Binding Ability of Recombinant SUMO-VEvhh10 with VEGF RBD 8-109
To verify the binding ability of recombinant SUMO-VEvhh10 to VEGF, an ELISA-based immunoassay was utilized according to the method described earlier. The results of the dose-response curve of VEvhh10-SUMO expressed using the ELISA method (Fig. 8) demonstrated that as the VEGF concentration increased, more anti-VEGF molecules were attached, resulting in increased light absorption.
DISCUSSION
The success of this study in amplifying, cloning, and expressing the VEvhh10 and SUMO genes underscores the utility of pfu polymerase and enzyme-based digestion for accurate gene construction as depicted in (Fig. 1), (Fig. 2), (Fig. 3) and (Fig. 5). The transformation of the ligated products into E. coli DH5α and subsequent colony PCR verification demonstrate that this method is efficient for cloning single-domain antibodies like VHH. The ability to amplify and clone the VEvhh10 gene with precision using pfu polymerase is consistent with earlier reports, which highlight the enzyme’s high fidelity in DNA replication and amplification compared to Taq polymerase. This methodological choice was critical in ensuring the accuracy of the VEvhh10 sequence during amplification (34). Moreover, the fusion of SUMO to VHH played a crucial role in enhancing the soluble expression of VHH. Previous studies have shown that recombinant VHHs often suffer from poor solubility and tend to aggregate into inclusion bodies when expressed in E. coli (35). The presence of SUMO, a small ubiquitin-like modifier, aids in overcoming this limitation by acting as a solubility-enhancing partner. SUMO fusions not only improve the solubility of the target nanobodies but also stabilize it during expression in bacterial hosts (36). In this study, SUMO fusion resulted in high yields of soluble VHH, which was efficiently expressed and purified using Ni-NTA chromatography with purity exceeding 90% as depicted in (Fig. 6) and (Fig. 7). This high purity, confirmed by SDS-PAGE, highlights the effectiveness of SUMO in both solubility enhancement and streamlined purification using His-tag. The successful production of recombinant VEGF 8-109 and its biological activity in promoting HUVEC proliferation further supports its use in functional assays. The MTT assay results, showing increased cell proliferation in response to VEGF 8-109, are consistent with previous research that indicates the importance of VEGF in promoting angiogenesis and endothelial cell growth (34). This validates the functional integrity of the expressed VEGF 8-109, suggesting that it retains its biological activity post-purification. The recombinant VEGF 8-109 can now serve as a valuable reagent in future binding assays with VHH or other therapeutic antibodies targeting VEGF pathways. Furthermore, the ELISA-based binding assays confirmed that SUMO-VEvhh10 binds effectively to VEGF, with increasing concentrations of VEGF resulting in a corresponding increase in light absorption as depicted in (Fig. 8). This binding affinity is crucial, especially for applications where VHH antibodies might be used to inhibit VEGF-mediated signaling, which is implicated in pathological conditions such as cancer and age-related macular degeneration (39). The observed binding behavior is consistent with previous works where VHH antibodies, despite their small size, exhibit strong binding capabilities to their respective antigens. This reinforces the potential of SUMO-VEvhh10 as a therapeutic agent targeting VEGF-related diseases, and the use of the SUMO fusion strategy could offer advantages over traditional expression systems by improving stability, solubility, and yield. Comparatively, the SUMO fusion system has demonstrated its superiority over other solubility-enhancing tags such as GST or MBP in maintaining the bioactivity of recombinant proteins (40, 41). While GST and MBP are effective in promoting solubility, they can sometimes mask epitopes or interfere with downstream applications, making SUMO a preferable option in cases where antigen binding and bioactivity must be preserved (42). This study adds to the growing body of literature that underscores the effectiveness of SUMO fusion in producing functional and soluble VHH antibodies for therapeutic applications. Future work could focus on optimizing expression conditions to further enhance yield or test the efficacy of SUMO-VEvhh10 in animal models of VEGF-related diseases.
CONCLUSION
This study highlights the utility of SUMO Fusion Technology for enhancing the expression of VEvhh10 targeting VEGF in E. coli. The successful production of soluble VHH against VEGF underscores its potential for future therapeutic and diagnostic applications in various diseases.
INTRODUCTION
Electrophoresis is a method for separating charged particles under an electric field. Electrophoresis, in its various forms or types, has become the most widely used method for analyzing biological molecules in biochemistry or molecular biology, including genetic components such as DNA or RNA, proteins, and Polysaccharides [1] [2]. The high-precision of electrophoresis has made it an important tool for advancing biotechnology [3]. Agarose gel electrophoresis is a form of electrophoresis used to separate DNA fragments based on their size [4]. Under the influence of an electric field, fragments will migrate to either the cathode or the anode, depending on the nature of their net charge. It is the most common means of separating moderate to large-sized nucleic acids and has a wide range of separations [5]. And an effective method for separating, identifying, and purifying 0.5 to 25 kb DNA fragments. It is known that the mobility is independent of the size of DNA with the size ~400 base pairs (bp) and larger, and it varies with the ionic strength of the electrolyte solution used [6]. The development of gel electrophoresis as a method for separating and analyzing DNA has been a driving force in the revolution of molecular biology over the past 20 years [7]. These techniques are now used by thousands of researchers and laboratory workers. More than half of all scientific papers published in biochemistry currently rely on electrophoresis methods [8]. In principle, understanding DNA gels conceptually is easy and technically feasible. In practice, many small details affect the accuracy and repeatability of the results [7]. The electrophoresis of Agarose gel is typically carried out using either Tris acetate EDTA (TAE) or Tris boric acid EDTA (TBE) buffers [9]. Research has identified other effective solutions compared to the mentioned buffers, with sodium bicarbonate being one of the most important due to its wider availability and much lower cost than other buffers [10]. Many researchers have studied alternatives to gel agarose that are less costly, these studies have included: gelatin, agar, and corn starch [11] [12] [13].The use and study of plant-based gel has not been sufficiently explored in previous research, so we focused on this type of gel in our study as it can be more easily and readily sourced than agar gel and is relatively cheaper. It can be concluded that the effective use of plant-based gel may lead to a wider range of electrophoresis application.
MATERIALS AND METHODS
Preparation of 1 L of 1X TAE buffer from 40X stock In DNA-related biological experiments, buffers are used to maintain a constant physiological pH. The electrophoretic mobility of DNA has been found to be strongly buffer dependent with TAE buffer pH for DNA fragments being ]15[ ]14[ 8.0. A volume of 50 mL of 40X TAE (Promega®) was measured into a 2 L beaker and was topped up with 1950 mL of distilled water to obtain a working solution of 1X TAE. Preparation of agarose gel (positive control) Agarose, a strongly gelling polysaccharide, is a common ingredient used to optimize the viscoelastic properties of a multitude of food products. This polymer is composed of a repeating disaccharide unit called agarobiose, which consists of galactose and 3,6-anhydrogalactose [16] [17]. The concentration of agarose in a gel depends on the size of the DNA fragments, which are separated with most gels ranging from %0.5 to ]19[ ]18[ %2. 1 g of electrophoresis-grade agarose (Vinantis®) was added to 100 ml of electrophoresis buffer. The gel was then prepared by melting the agarose in a microwave oven or autoclave and swirling to ensure even mixing. Melted agarose should be cooled to 50-60°C under running tap water before pouring it onto the gel cast. Gels are typically poured between 0.5 and 1 cm thick. The volume of the sample wells is determined by both the thickness of the gel and the size of the gel well [20]. Preparation of corn starch gel To prepare boric acid and sodium hydroxide buffers, corn starch was modified by adding amount of 1.855 g of boric acid and 0.48 g of NaOH, which were added to a 1 L beaker containing 200 ml of distilled water and stirred to homogeneity. We added 36 g of corn starch to the mixture and topped up with distilled water to the 1 L mark. The solution was stirred very well and allowed to stand in a water bath at 50 °C for 30 min. the supernatant was discarded, and the precipitant was kept. Next, 30 ml of distilled water was added to the precipitant and stirred to homogeneity, and then the Beecher was set in a water bath until it was dried. The modified dry starch was then ground until it became powder. An amount of 12 g of the modified corn starch was weighed and added to a beaker containing 100 ml of 1X TAE and the beaker was placed in a water bath until boiling. The supernatant was discarded, and the precipitant was taken and poured into the gel cast with the combs in place, and left until it solidified [13]. Preparation of Animal gelatin gel An amount of 1 g of animal gelatin powder was weighed and added to a beaker containing 100 ml of 1X TAE buffer. It was mixed well and microwaved for 2 minutes, with stopping every 30 s to gently mix it. The solution was cooled underwater. The gel was then poured into the gel cast. This protocol is commonly used in research. Preparation of an agar–animal gelatin gel mixture An amount of Agar (0.5 g) and animal gelatin (0.5 g) were weighed and added to a beaker containing 100 ml of 1X TAE buffer. The remaining steps are as mentioned in the animal gelatin gel. Preparation of %1 Agar gel An amount of 1 g of Agar was weighed and added to a beaker containing 100 ml of 1X TAE buffer. The remaining steps are identical to those for animal gelatin gel. Preparation of 1 L of sodium bicarbonate (SB) buffer Sodium borate is a Tris-free buffer with low conductivity. Therefore, gels can be run at higher voltages. SB produces sharp bands and nucleic acids can be purified for all downstream applications. However, SB is not as efficient as Tris-based buffers for resolution bands larger than 5 kb. Under standard electrophoretic conditions, SB provided resolution and separation as good as or better than TBE and TAE gels [21] [22]. A volume of 2 g of sodium bicarbonate, 0.12 g of NaOH and 0.05 g of NaCl was poured into a 1 L beaker and was topped up with 1 L of water to obtain a working solution of SB buffer [10]. Preparation of 1.5 % food grade agar-agar gelatin gel An amount of 3.75 g of food grade agar-agar gelatin powder was weighed and added to a beaker containing 250 mL of SB buffer. It was mixed well and microwaved for 2 minutes, with stopping every 30 seconds to gently mix it to avoid bubbles. The solution was cooled underwater. The gel was then poured into the gel cast. A 15 well comb was inserted, and the gel was left to solidify. The comb was gently removed, and the gel was placed in a horizontal gel tank. Sodium bicarbonate buffer was added to the gel tank at the maximum mark. Loading samples into modified corn starch %1 gel and agar – animal gelatin mixture %1 gel Loading ten microliters (10 µl) of human genomic samples [23] [24] after mixing them with 3 microliters (3 µl) of loading dye for all wells. The gel was placed in the tank containing 1X TAE buffer, passed through an electric current of 60 V for 5 minutes and then increased to 95 V for 1 hour. Afterward the gel was removed from the horizontal gel tank and dyed in Ethidium Bromide for 30 minutes because ethidium bromide (EtBr) is sometimes added to the running buffer during the separation of DNA fragments by agarose gel electrophoresis. It is used because when the molecule is bound to the DNA and exposed to a UV light source [25], Ethidium binds strongly to both DNA and RNA at sites that appear to be saturated when one drug molecule is bound for every 4 or 5 nucleotides [26]. It is then transferred to a tank of water with mild shaking for washing for 2 minutes. The gel was removed and viewed using a gel documentation device (UVP BioDoc-It). Loading Samples and Electrophoresis The DNA molecular weight standard control, also called the DNA marker (Ladder), the DNA ladder was separated by conventional agarose gel electrophoresis [27] [28]. Loading 10µL of human genomic samples after mixing them with 3µL of loading dye for wells 3 ,2 ,1 and 4, and 3µL of 50 bp DNA Ladder (vivantis®) in the fifth well. The electrophoresis involved the following steps: First, the voltage was 30 V for 5 minutes, the volt was increased to 45 V for 5 minutes, then to 60 V for 5 minutes, then to 70 V for 10 minutes, then to 90 V for 1 hour and a half (1.5 h). At the end, the voltage was increased to 95 V for 45 minutes in order to avoid DNA escaping from the wells. The gel was removed from the horizontal gel tank and dyed in Ethidium Bromide for 30 minutes and then transferred to a tank filled with washing water for 2 minutes. The gel was removed and viewed using a gel documentation device (UVP BioDoc-It). This protocol was performed for the %1 agarose gel and %1.5 treated food grade agar-agar gel.
RESULTS
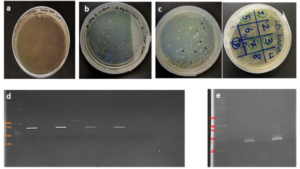
Electrophoresis was performed for human genome samples, and a ladder of agarose gel with TAE solution was used as a control for the studied samples: Corn starch gel with TAE solution, agarose gel with TAE solution, animal gelatin with TAE solution, agar with TAE solution, agar – animal gelatin mixture with TAE solution, and food grade agar-agar gelatin with a solution of sodium bicarbonate sodium hydroxide and sodium chloride. All experiments were carried out under similar conditions of pH and using the same equipment and tools. Many aspects were compared during the experiment on a repetitive level, and a mean of duration of solidification, texture, color, dye duration and other parameters are mentioned in Table1.
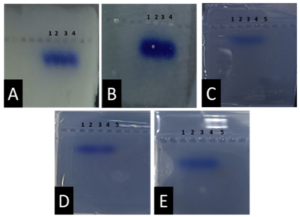
From Figure 1 we find that the animal gelatin gel (c) forms a surface ice layer and is not fully hardened. One of the reasons for this is the very low heat and low concentration of animal gelatin. Corn starch gel (B) gave a white color and similar properties in terms of the structure with agarose gel. Other gels gave properties in structure and color very similar to agarose gel.

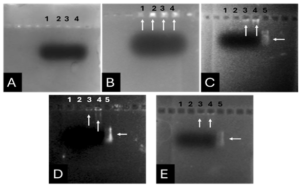
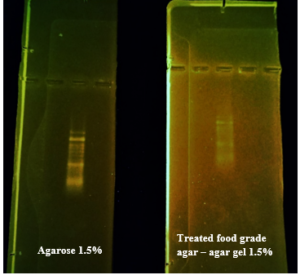
Before the samples were exposed to UV radiation, we can see from Figure 2 that the loading dye was electrophoresed for a distance of 1.2 cm in corn starch gel (A), for a distance of 1.7 cm in agar – gelatin mixture gel (B), for a distance of 0.9 cm for the loading dye and 1.3 cm for the Ladder in agar gel (C), for a distance of 1.4 cm for the loading dye and 1.7 cm for the Ladder in agarose gel (D), for a distance of 1.2 cm for the dye and 1.7 cm for the Ladder in treated food grade agar – agar gel (E) at the voltage and time shown in Table 1 for each gel mentioned. After the electrophoresis of 12% modified corn starch gel, 1% agar – animal gelatin mixture gel, 1% agar gel, 1% agarose gel, and 1.5 % of our treated food grade agar-agar gel with BS buffer, a separation of DNA was apparent, as shown in Figure 3, the modified Gel that is annotated with (E) in the Figure 3 shows good separation of the 50 bp DNA ladder (Vivantis®) in the 5th well, and the 4th well in E is genomic DNA extracted from human saliva. As for agarose gel D in Figure 3, good separation occurred in the 5th well and it showed resemblance to agarose gel in C. The gels were exposed to ultraviolet radiation and examined; we noticed that the disappearance of the fluorescence from the treated food grade agar-agar gel after 15 minutes, while the agarose retained its fluorescence for 25 minutes before the bands vanished from the UV. Knowing that the gels were dyed with the same type and concentration of dye and duration of time. For an electrophoresis buffer consisting of sodium bicarbonate, sodium hydroxide, and sodium chloride, it has shown high efficiency in securing the ions needed for electrophoresis while maintaining its physical and chemical properties; thus, it can be considered an equivalent solution to TAE solution. These results demonstrate the effectiveness of this variant using human genomic DNA. Electrophoresis with a ladder marker gave good results and good separation, as shown in Figure 4, which displays a comparison between agarose 1.5% and the treated food grade agar-agar gel 1.5%, where 5 µl of the marker was loaded into the wells in both gels at 40 V for 5 minutes and 80 V for 2 h followed by 30 minutes of soaking in an ethidium bromide tank. The results showed acceptable efficiency for the treated food-grade agar-agar similar to the efficiency of the agarose gel with some modifications in the method of work. Further enhancements of the images using gel documenting software could even make the separation look clearer for the treated food-grade agar -agar gel.
DISCUSSION
This research addressed finding a frugal alternative for agarose used in agarose gel DNA electrophoresis. The alternatives experimented in this research included: Agar, which originated in Japan in 1658. It was first introduced in the Far East and later in the rest of agarophyte seaweed-producing countries [29]. Agar is obtained from various genera and species of red–purple seaweeds—class Rhodophyceae—where it occurs as a structural carbohydrate in the cell walls and probably also plays a role in ion-exchange and dialysis processes [30]. Agar is a natural polymer commonly used in various fields of application, ranging from cosmetics to the food industry [31]. It is a gel forming polysaccharide with a main chain consisting of alternating 1,3-linked β-d-galactopyranose and 1,4-linked 3,6 anhydro-α-l-galactopyranose units [32]. Agarobiose is the basic disaccharide structural unit of all agar polysaccharides. Agar can be fractionated into two components: agarose and agaropectin [33]. The food-grade agar results were similar to agar results, yet microbiological agar can be more costly compared to food-grade agar-agar, and the treatment of agar with different salts described in this method gave slightly better results from previous research [12]. We also tested Starch, which is a major food source for humans. It is produced in seeds, rhizomes, roots, and tubers in the form of semi-crystalline granules with unique properties for each plant [34]. Edible and industrial corn starch was modified and used to prepare the electrophoresis gel. Corn starch is composed of two large α-linked glucose-containing polymers. Namely, smaller and nearly linear amylose and very large and highly branched amylopectin [35]. The starch alternative gel didn’t give good results and it was difficult to handle and too thick, so no DNA bands appeared [13]. Another alternative tested was Gelatin, which is a protein obtained by partial hydrolysis of collagen, which is the chief protein component in the skin, bones, hides, and white connective tissues of the animal body [36]. We can conclude from the gelatin gel result that it is not a good candidate for DNA gel electrophoresis, and this has been the case since the late 1980s.[11] From the results shown in Fig. 1, we can conclude that modifying the materials concentration allows us to control the structural and solidification properties. It is important to consider the appropriate gel concentration for the gel’s retinal structure, which is where electrophoresis samples pass, and this is in accordance with Bertasa et al. 2020 research that describes a stronger gel formation and crosslinks with increasing the concentration and anhydro units in the gel in addition to alterations of appearance and color, yet this didn’t apply to gelatin and starch where gelatin lacked the strength to solidify and the starch was too thick and difficult to handle after pouring because it solidified very quickly. [37] We can observe that the previously mentioned gels in Fig. 2 resulted in the electrophoresis of dyes at least, and this is logical because these gels create a charge neutral trap for the negatively charged loading dye to pass through in the presence of an electric field and an electrolyte. [38] From our results shown in Table 1, treated food grade agar-agar gel prepared with sodium bicarbonate solution was the most closely related alternative to the commonly used agarose gel with modifications in the working method to achieve very close results with agarose, while starch gel failed to give a proper result. Also, the mixture didn’t give a clear result because the DNA samples couldn’t get out of the wells. Agar gel, the same as agar – agar gel, gave results similar to those of agarose. But still, treated agar – agar gel showed better results than agar gel by the distance crossed by the DNA samples and the display of the samples, in addition to the low cost. This result of genomic DNA electrophoresis is well known and is confirmed by several previous researches, such as Green et al. 2019, where large genomic DNA fragments migrate slower than smaller fragments, and smearing marks in the resulting gel image refer to poor-quality DNA or electrophoresis conditions. [39] As for cost, 1 g of agarose costs around 35,000 Syrian pounds, while 1 g of agarose costs almost 2000 Syrian pounds, while 1 L of TBE 1x costs nearly 700,000 Syrian pounds, while SB buffer roughly costs 3500 Syrian pounds for the same amount, this makes this alternative 15 times cheaper than agarose gel, and 200 times cheaper for the electrolyte used. It seems from Fig. 4 that the treated food grade agar-agar can show strong bands from the ladder, and the separation requires more time; hence, it could be recommended to use it for PCR products of one band and a ladder with several strong bands, and the background fluorescence from ethidium bromide on the treated gel could mean that there should be more rinsing time for it, in order to give clearer bands.
Conclusions and Recommendations
This study offers a very low-cost alternative to agarose gel to help laboratories with limited income. We found that treated food grade agar-agar could give similar results to those of agarose gel, and by using other buffers for electrolyte like SB buffer. Based on the results of this study, this method provides a low-cost alternative to agarose and TBE & TAE, and it can be used by low-budget labs with limited budgets to make DNA assays more domesticated, where the alternatives suggested here cost 15 times less than the industrial agarose and electrolytes. Further research is recommended to enhance the clarity of the gel and explore the potential applications of this new gel in RNA separation and plasmid DNA separation and PCR amplicons of different lengths.


Journal:![]() Syrian Journal for Science and Innovation
Syrian Journal for Science and Innovation
Abbreviation: SJSI
Publisher: Higher Commission for Scientific Research
Address of Publisher: Syria – Damascus – Seven Square
ISSN – Online: 2959-8591
Publishing Frequency: Quartal
Launched Year: 2023
This journal is licensed under a: Creative Commons Attribution 4.0 International License.